📌 학습목표
- 페이지랭크 알고리즘이 어떻게 동작하는지
- 페이지 랭크의 문제점과 이를 해결할 수 있는 알고리즘
- 전파를 모델링 하는 간단한 수학적 모형들
- 주어진 그래프와 규칙에서 전파를 최대화 하는 천파 최대화 문제에서 어떻게 전파가 이루어지는지
📌검색엔진 Google 의 시작
이 블로그에서 랭크 알고리즘에 대해 되게 멋지게 설명한다.
“Google”이라는 230조원짜리 회사가 처음 시작된 곳이 바로 이 세르게이 브린과 래리 페이지가 쓴 논문(The Anatomy of a Large-Scale Hypertextual Web Search Engine)이었다"
구글 이전의 검색엔진은 웹을 거대한 디렉토리로 정리했다.
블로그를 쓰는 사람이라면 알겠지만, 자신의 블로그를 하나의 디렉토리로 정하는 게 상당히 어렵다. 나만 그런가?
그거와 비슷하게 디렉토리로 정하게 되면 카테고리의 구분도 모호해지고, 수십억~수백억개로 웹페이지의 수가 증가함에 따라 카테고리의 수와 깊이도 무한정 커지는 문제점이 있다.
그 다음에는 웹페이지에 포함된 키워드에 의존한 검색엔진이 나왔다.
하지만 의도적으로 성인사이트에서 "축구"라는 키워드를 보이지 않도록 여러 번 포함하게 되면 "축구"를 검색하면 해당 성인사이트가 결과로 나오게 될 수도 있다.
웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성 있는 그래프라고 생각할 수 있다.
웹페이지는 정점으로, 하이퍼링크는 나가는 간선에 해당된다.
내가 내 블로그에 저 위 ↑의 블로그들을 하이퍼링크로 달았기 때문에, 내 블로그가 하나의 정점이라면 저 하이퍼링크들은 위의 블로그들이라는 정점과 연결해주는 간선이 된다.
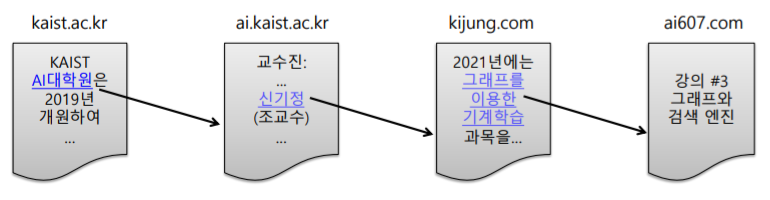
페이지랭크는 이런 웹과 하이퍼링크의 관계를 이용하여 검색 한다.
페이지랭크(Pagerank)는 다른 페이지에서 오는 링크를 같은 비중으로 세는 대신에 , 그 페이지에 걸린 링크의 개수를 normalize하는 방식이다.
📌 페이지랭크의 정의 : 투표관점
위 그림처럼 어떤 웹페이지 u가 웹페이지 v로의 하이퍼링크를 포함한다면, u가 v에게 투표했다고 간주한다.
그리고 이런 투표를 많이 받을 수록 사용자의 키워드와 관련성이 높고, 신뢰할 수 있는 웹페이지가 된다.
들어오는 간선(자신을 하이퍼링크 참조한 웹페이지들)이 많을 수록 이 웹페이지는 신뢰할 수 있게 된다.
어려운 얘기가 아니다. 평소 맛집을 갈 때 사람들은 네이버,인스타 등에 검색을 통해 사람들의 후기가 많은 곳에 가게 된다. 후기가 많을 수록 믿을만한 맛집이라고 생각하기 떄문이다. 어떤 식당에 대한 후기가 곧 사람들이 식당에 투표를 한 것이고, 그런 투표(후기)가 많을수록 신뢰할 수 있는, 믿을만한 식당이 되는거다.
근데 요새 네이버에 맛집 검색을 잘 안한다. "광고"가 너무 많기 때문이다. 사람들의 후기는 많은데 다 악의적인 광고다.
그렇기 때문에 내가 진짜 필요한 맛집 정보가 아니게 된다.
웹페이지도 똑같다. 이 문서가 많이 하이퍼링크 참조(들어오는 간선)이 될 수록 신뢰할 수 있을까? 아니다.
악의적인 광고?와 같이 들어오는 간선 수를 부풀어 관련성과 신뢰도가 높아보이게 악용하는 것일 수도 있다.
인스타와 같은 SNS를 하다보면 월 2달러에 팔로우를 늘려드립니다!와 같은 광고가 그런 예이다.
그럼 단순하게 들어오는 간선(하이퍼링크 참조)가 많으면 신뢰성 있는 웹페이지라고 보긴 힘들다.
그렇기 때문에 "가중투표"를 하게 된다. 관련성이높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주하는 거다.
만약 대통령이 "나"를 추천한다면, 많은 사람들이 오~ 저 녀석 채용해버리고 싶은데? 싶지만, 나같은 일반시민이 여러 사람을 추천해주면 아무도 믿지 않는 것과 같은 원리다.
측정하려는 웹페이지의 관련성 및 신뢰도를 페이지랭크점수 라고 부르자.
각 웹페이지는 각각의 나가는 이웃에게 자신의 페이지랭크 점수/ 나가는 이웃의 수만큼 가중치 투표를 한다.
만약 내 페이지랭크 점수가 90점일 때, 위에 하이퍼링크를 3곳 달았으니까, 각각의 웹페이지에 90/3 = 30만큼 투표하는거다.
아래 그림을 예시로 들어보면 j는 i,k에게 투표를 받고 있다.
i는 나가는 이웃의 수가 3개이니, 자신의 랭크 점수를 나가는 이웃의 수로 나눈 $\frac{r_{i}}{3}$만큼을 j에게 투표한다.
k는 나가는 이웃의 수가 4개이니, $\frac{r_{k}}{4}$만큼을 j에게 투표한다.
j의 페이지랭크 점수는 $r_{j}=\sum_{i \in N_{in(j)}}\frac{r_{i}}{d_{out}(i))} $ 이 된다.
풀어쓰면 j로 들어오는 정점들에 대해서, 그 정점들의 랭크를 정점들이 나가는 이웃의 수만큼으로 나눠준 값들의 합이다.

📌 또 다른 관점 : 임의 보행 관점 ( Random Walk)
웹서퍼가 현재 내 웹페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 웹을 서핑한다고 해보자.
현재 페이지에 하이퍼링크가 3개니깐 각각의 링크를 1/3확률로 클릭하는 거다.
웹서퍼가 t번째 방문한 웹페이지가 웹페이지 i일 확률을 $p_{i}t$라고 한다.
P(t)는 길이가 웹페이지 수와 같은 확률분포 벡터가 된다. t번쨰에 각각의 웹페이지로 넘어갈 확률 v개를 담고있다.
그러면 t+1번째에 j번째 웹페이지에 방문할 확률은 어떻게 될까?
그러려면 기본적으로 t번째에 방문한 웹페이지들이 j번쨰 웹페이지와 연결되어있어야한다.
위의 그림으로 따지자면 t번째에 i 혹은 k 웹페이지와 같이 j로 갈 수 있어야지만 t+1번째에 j웹페이지에 방문 할 수 있다.
그럼 결국 t+1번째에 j번째 웹페이지에 방문할 확률은 t번째에 j로 나갈 수 있는 웹페이지들의 확률의 합이 된다.
$p_{j}(t+1)=\sum_{i \in N_{in(j)}}\frac{p_{i}(t)}{d_{out}(i)} $
이 과정을 무한히 반복해, t가 무한히 커지면 결국 p(t) = p(t+1) = p로 수렴하게 되고, 이를 정상분포라고 한다.
결국 투표관점에서의 페이지 랭크 점수와 임의 보행 관점에서의 정상분포는 동일하다.

📌 페이지 랭크의 계산
결국 페이지 랭크는 어떤 관점에서 보나 구하는 식은 같아진다.
페이지랭크 점수는 재귀적으로 계산되므로, 일정 값으로 수렴할 때 까지 반복해서 구해줘야한다.
임의 보행 관점에서 보면 무한히 반복해 p라는 값으로 수렴시켜 정상분포를 얻어내야한다.
반복곱 (power iteration)을 사용해 페이지랭크를 계산할 수 있다.
- 각 웹페이지의 페이지랭크 점수 $r_{i}^{0}$을 동일하게 1/웹페이지수로 초기화해준다.
- 페이지랭크 점수 식을 이용하여 페이지랭크 점수를 갱신한다.
- 수렴하면 종료한다. 수렴하지 않았다면 2번 과정을 반복한다.

맨 처음에는 1/3로 모두 똑같다.
y는 자기자신 y와 a로 나가므로 자신의 점수 1/3을 2로 나눠 각각에게 전달한다.
a는 y와 m으로 나가므로 자신의 점수 1/3을 2로 나눠 각각에게 전달한다.
m은 a에게만 나가므로 자신의 점수 1/3을 그대로 a에게 전달한다.
그러면 y는 a로부터 받은 1/6 , 자신으로부터 돌려받은 1/6을 더해 1/3이 된다.
a는 y로부터 받은 1/6 , m으로부터 받은 1/3을 받아 1/2이 된다.
m은 a로부터 1/6을 받아 1/6이 된다.
이런 과정을 각각의 페이지랭크 점수가 수렴할 때까지 계속 반복한다.

임의 보행 관점에서 바라봤을 때, 각각의 최종 페이지랭크 점수들은 합이 1이 되어 확률의 조건을 만족시킨다.
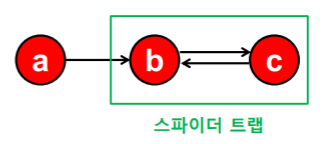

하지만 이런 경우 페이지랭크 점수는 수렴하지 않는다. {b,c}처럼 들어오는 간선은 있지만 나가는 간선은 없는 정점 집합때문에 수렴하지 않는 문제를 스파이더 트랩에 의한 문제라고 한다.
반복곱은 항상 수렴하는 것을 보장할 수 없다.

b처럼 들어오는 간선은 있지만 나가는 간선은 없는 "막다른 정점"일 경우 모두 랭크가 0으로 수렴해버린다.
반복곱은 "합리적인"점수로 수렴하는 것을 보장할 수 없다.
📌 순간이동 : 페이지 랭크의 문제 해결사
결국 위 두개의 문제점은 들어오는 간선은 있지만, 나가는 간선이 없기 때문에 생기는 문제들이다.
"순간이동"이라는 개념을 도입하면 문제를 해결할 수 있다.
- 웹페이지에서 하이퍼링크(나가는 간선)이 없다면 , 임의의 페이지로 순간이동한다.
- 하이퍼링크가 존재한다면 $\alpha$의 확률로, 존재하는 하이퍼링크들 중 하나를 균일한 확률로 클릭한다.
- 1-$\alpha$의 확률로 임의의 페이지로 순간이동한다.
이런 식으로 순간이동을 하게 되면 나가는 간선이 무조건 생기게 돼 스파이더 트랩이나 막다른 정점에 갇히는 일이 없어진다. 이 $\alpha$를 감폭비율 혹은 damping factor라 하고 0.8~0.85 정도를 사용한다.
순간이동을 고려하게 되면 식은 다음과 같이 바뀐다. $\alpha$의 확률로 이전 정점들의 나가는 간선으로 선택됐을 때와 , 순간이동에 의해 1-$\alpha$의 확률로 모든 정점 v개 중 하나로 선택됐을 때의 합으로 구성된다.

아래 보라색 동그라미들은 들어오는 간선은 없지만 순간이동에 의해 1.6이라는 페이지랭크 점수를 가지게 된다.
빨간색 B는 당연히 들어오는 간선이 많으므로 페이지랭크 점수가 크다.
주황색 C는 들어오는 간선은 하나밖에 없지만 가장 큰 점수를 가지고 있는 B가 C에게 몰빵해주기 때문에 크다.

📌개인적인 생각
페이지랭크를 계산할 때, 1/웹페이지수인데, 웹페이지수가 수만수억개면 컴퓨터는 이를 0으로 계산하지 않을까?
하이퍼링크로만 모든 것을 계산한다,,,? 하이퍼링크만을 어떻게 신뢰도를 계산하지?
아무리 좋은 글이어도 불펌을 많이해가면 문제가 되지않나?
=> 역시 페이지랭크는 옛날 방식이고, 요새는 유입자 수 , 검색어 키워드 , 머물고 있는 시간, 글의 길이, 사진 갯수 등 여러 개를 고려해서 신뢰도를 매긴다고 한다.
📌 그래프를 통한 전파의 예시
- 온라인 소셜 네트워크 : 정보, 행동 ex) 아이스버킷챌린지
- 컴퓨터 네트워크, 파워 그리드 : 정전
- 사회 : 질병 ex) 코로나
전파의 대상도, 과정도 다양할 뿐만이 아니라 매우 복잡하다.
이를 체계적으로 이해하고 대처하기 위해 수학적 모형화가 필요하다.
이게 왜 필요하냐고 물어본다면 지금 시국을 생각해보자.
확진자의 전파를 막기 위해서는 이를 대처하기 위한 어떤 모델링이 필요하다.
📌 의사결정 기반 전파 모형
주변 사람들의 의사결정을 고려하여 각자 의사 결정을 내리는 경우 의사결정 기반의 전파모형을 사용한다.
실제 상황에서 주변 사람들의 의사 결정을 고려하는 경우는 무엇이 있을까?
거의 카카오톡을 사용하므로, 카톡이 아닌 라인을 쓴다면 주변 사람들과 소통할 수 없으므로 나도 따라서 카톡을 쓴다.
혹은 주변 사람들이 다 아이패드가 좋다 좋다 다들 사니까 나도 따라 산다.
이런 경우가 주변 사람들의 의사결정을 고려하는 의사결정 기반 전파모형이다.
그 중 특정 임계치를 넘으면 의사결정이 바뀌는 선형임계치모델을 생각해보자.
내가 u고 이웃들 중 2명은 A를 3명은 B를 선택했다고 할 때, 아주 단순하게 베프 이런 거 없이 모든 친구들과의 사이는 똑같고 나도 A를 사용하면 a만큼의 효용이, B를 사용하면 b만큼의 효용이 생긴다고 하면
A를 선택하면 2a가 B를 선택하면 3b만큼의 효용을 얻을 수 있다.

그럼 나는 뭘 선택할까???? 당연히 더 큰 쪽을 선택하게 된다.
그렇기 때문에 이를 일반화하면 전부 B를 사용한다고 가정하고, 다들 폴더폰을 쓴다고 해보자. 갑자기 초6으로 돌아가기
새로 나온 스마트폰을 사용하는 얼리어답터들을 A라고 가정한다.
그러면 이 A들을 시드집합(SEED Set)이라고 하며 이 사람들은 곧 죽어도 A를 고수한다.
내 이웃 중 P만큼 스마트폰 (A)를 선택했다면, 1-P만큼은 아직 폴더폰(B)이다.
그러면 나는 언제 스마트폰을 살 수 있을까? 친구들이 웬만큼 스마트폰을 사서 나만 폴더폰일 수 없을 그 때다.
ap > b(1-p)를 만족할 때, 이때 스마트폰으로 바꾸게 된다.
이를 p에 대해 풀게 되면 $\frac{b}/{a+b}$가 되고 이를 임계치 q라고 한다.
이웃 중 A를 선택한 비율이 임계치 q를 넘을 떄만 A를 선택하게 된다.
아래는 선형임계치모형에 의해 전파되는 과정이다.
1번에서 u,v가 seed set이고, 임계치가 55%라고 설정했을 떄, 자신의 이웃노드 중 55% 이상이 A면 자신도 A라는 의사결정을 하게된다. 그런 식으로 6번까지 전파가 되고 6번 과정에서는 맨 마지막에 남은 두 노드는 아무리 반복해도 임계치를 넘지 않으므로 이 둘은 평생 폴더폰을 쓰게 된다,,,,
보통 얼리어답터가 20대인 걸 생각하면 20대들은 유행에 따라서 빠르게 바뀌지만, 할머니들은 20대들과의 연결이 많지 않아 계속 폴더폰을 쓰는 경우를 생각하면 어떨까 싶다.

📌 확률적 전파 모형
내 의사와는 상관없이 전파되는 경우도 있다. 바로 코로나,,,,
누구도 코로나에 걸리기로 의사결정하지 않으므로 이런 경우 대해서는 의사결정 전파모형을 사용할 수 없다.
이 경우는 확률적 전파 모형인 독립전파모형으로 설명할 수 있다.
코로나를 생각해보면 감염시키는 사람과 감염당하는 사람이 있고, 마스크를 어떻게 쓰냐에 따라서 감염될 확률이 달라진다. 이런 점을 고려해서 방향성이 있고, 가중치가 있는 아래와 같은 그래프를 고려해보자.

간선 (u,v)의 가중치 $p_{uv}$는 u가 감염되었을 때, u가 v를 감염시킬 확률에 해당된다.
즉 , 정점 u가 감염될 때, 각 이웃 v는 $p_{uv}$의 확률로 전염된다.
이때 서로 다른 이웃이 전염되는 확률은 독립적이다. 내가 내 친구를 감염시켰다고, 내 직장동료도 감염되지는 않기 때문이다.
마찬가지로 최초 감염자들을 시드집합이라고 부른다.
최초 감염자는 각 이웃들에게 간선에 해당하는 확률로 병을 전파하고, 새로운 감염자 각각이 반복하게 된다.
이때 시드집합이 중요하다. 만약 시드집합이 맨날 방구석에 있는 나같은 사람이면, 영향력이 없기 때문에 새로운 감염자는 거의 생기지 않는다. 하지만 시드집합이 매일 밖에 마스크도 잘 안끼고, 밖에 나돌아다니는 사람이라면 영향력이 엄청 나기 때문에 빠르게 확산된다. 이런 슈퍼전파자들,,,,
📌 바이럴 마케팅 (casacade)
: 소비자들로 하여금 상품에 대한 긍정적인 입소문을 내게 하는 기법
(개인적인 생각) 바이럴 마케팅은 확률적 전파모형보다는 의사결정 기반 전파모형으로 설명할 수 있다.
무엇을 구매하거나, 챌린지는 나도 모르게 하는 게 아니라, 누군가를 보고 내 행동을 결정하는 거기 때문이다.
그렇기 때문에 입소문의 시작점이 되는 시드집합이 중요하다. 입소문을 처음 누가 내냐에 따라 전파되는 범위가 영향을 받기 떄문이다. 팔로워 10명이 광고하는 것보다는 팔로워 100k 같은 인플루언서 같은 사람들이 광고하는 게 더 많은 사람들이 영향을 받고, 입소문이 더 단시간내에 멀리 퍼지게 된다.
현재 시드집합인 u,v는 이웃이 5,6명으로 인싸 of 인싸다. 이럴 경우 단 하루만에 9명이 A를 선택하게 된다.

하지만 시드집합으로 x,y를 선택하게 되면 각각은 이웃이 1명 뿐이고 추가 전파는 발생하지 않게 된다.

그렇기 때문에 돈을 주고 홍보하는 기업들 입장에서는 같은 비용을 주더라도 더 많이, 더 빨리 전파할 수 있는 사람 즉, 전파력이 좋은 시드집합을 찾고싶어한다.
📌 전파최대화
그래프, 전파모형, 시드집합의 크기가 주어졌을 때, 최대화 할 수 있는 시드집합을 찾는 문제를 전파최대화라고 한다.
이는 굉장히 어려운 문제다. 간단하게 총 10000명의 사람 중에서 인플루언서를 10명만 뽑는다고 생각해도 생각되는 경우의 수는 2,743,355,077,591,282,538,231,819,720,749,000개다.
전파 최대문제는 NP-난해가 된다.
그래서 똑똑한 과학자들은 최고시드집합을 찾는 것을 포기한다 ^_^
대신 쉬운 방법으로 근사할 수 있는 방법을 찾게 된다.
- 정점 중심성 휴리스틱
시드 집합의 크기가 K개로 고정되었을 때, 정점의 중심성이 높은 순으로 K개를 선택하는 방법이다.
굉장히 합리적이지만, 최고라는 보장은 없다.
정점의 중심성은 페이지랭크 점수일 수도 있고, 직접 연결된 노드의 개수만을 세는 연결정도 중심성 일수도, 이외의 근접 중심성, 매개 중심성 기준으로 산정한다.
- 탐욕 알고리즘 (Greedy Algorithm)
조합의 효과등은 고려하지 않고. 근시안적으로 딱 그 순간 최대가 되는 조합을 뽑는 방법이다.
최초 전파자를 한 번에 한 명씩 선택한다.
정점이 v개라고 할 경우 1번부터 V번까지 고려해 전파를 최대화하는 시드 집합 x를 찾는다.
이때 시뮬레이션을 반복한 평균 값을 사용해서 전파의 크기를 비교한다.
그러면 {x,1} , {x,2} ,,,{x,v}같이 v-1개 중 x와 같이 시드집합이 되었을 때, 전파를 최대화하는 원소를 찾는다.
이런 과정을 목표하는 크기의 시드집합이 될 때까지 반복한다.
독립 전파 모형의 경우, 이론적으로 정확도가 일부 보장된다.
하지만 그렇다고 최고를 보장할 수 있는 것은 아니다.
'Naver Ai Boostcamp' 카테고리의 다른 글
| [Day 23.5] 추천시스템 (기초 ~ 심화) (0) | 2021.02.26 |
|---|---|
| [Day 23] 군집 탐색 (0) | 2021.02.24 |
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
| [DAY 20] self-supervised pretrained model - Bert , GPT (0) | 2021.02.20 |
| [DAY 19] Transformer (0) | 2021.02.18 |