군집 구조 분석
📌 군집 구조와 군집 탐색 문제
- 군집 : 군집(Community)이란 다음 조건들을 만족하는 정점들의 집합
- 집합에 속하는 정점 사이에는 많은 간선이 존재
- 집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재
- 실제 그래프에서도 군집들은 사회적 무리 / 조직 내 분란 등을 표현
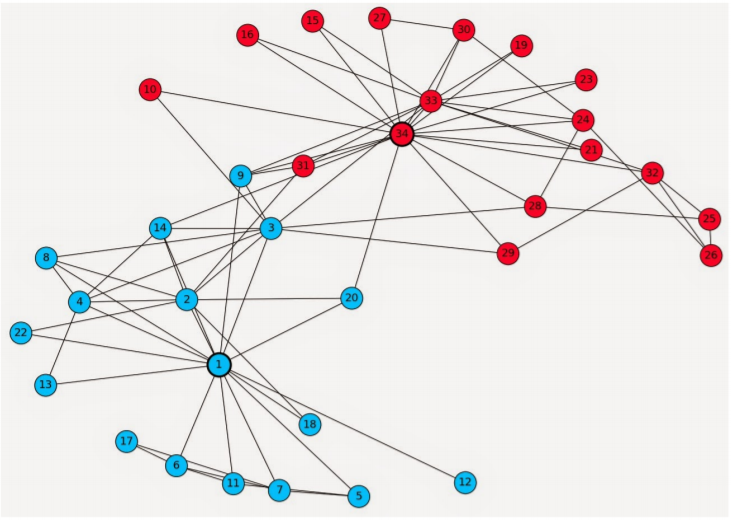
- 군집탐색문제(community detection)
: 그래프를 여러 군집으로 '잘' 나누는 문제, 클러스터링과 유사하지만 나뉘는 개체가 "정점"
그렇다면 "잘 나눴다"의 기준은 뭘까?
📌 군집 구조의 통계적 유의성과 군집성
-
배치모형
1 ) 각 정점의 연결성(Degree)를 보존한 상태 , 2 ) 간선들을 무작위로 재배치 하여 얻은 그래프를 의미한다.
각 정점에서 나가는 , 들어오는 간선의 수는 유지하되, 랜덤으로 정점들의 자리를 바꾼 그래프를 의미한다.
배치 모형에서 임의의 두 정점 i와 j 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례한다.
❓❓❓❓❓❓❓❓ 왜 확률이지? 무조건 생기는 거 아닌가? 라고 생각했는데 configuration model에 대한 다른 설명
cofiguration모델은 실제 그래프와 노드수 , 간선 수 , 연결성 분포(degree distribution)이 같아야 한다.
degree distirbution,,,,? 쫄지말자 실제 그래프 기준으로 21일에 배운 연결성의 두터운 꼬리분포를 의미하는거다.

spoking, switching 등의 configuration model을 만드는 방법이 있는 거 같은데, 내가 찾던 건 switching
A→B , C→D 를 쌍으로 서로 endpoint를 바꿔준다.
간선 수, 정점 수는 그대로 유지하면서 각각 정점의 연결성도 그대로 유지된다.
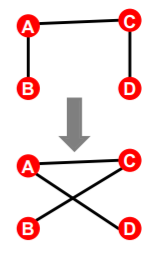
이제서야 "배치 모형에서 임의의 두 정점 i와 j 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례한다. " 이 말이 이해가 간다. A도 연결성이 높고, D도 연결성이 높으면, 둘이 1촌이 아니더라도 switching을 하다보면 1촌이 될 확률이 높아진다고 이해했다.
-
군집성의 정의
군집성 : 그래프가 얼마나 군집으로 잘 나누어져있는지에 대한 측정

- 군집성이 클 수록 군집탐색이 잘 되어있다는 뜻이다.
- 즉, 배치모형과 비교해 그래프에서의 군집 내부 간선 수가 월등히 많을 수록 성공한 군집탐색이다.
- 항상 -1과 1 사이의 값을 가지며, 0.3~0.7사이일 때, 유의미한 군집을 찾아냈다고 말할 수 있음.
내부 간선의 수의 기댓값은 어떻게 구하지?
우선 배치모형을 C라고 해보자. configuration model이라서 이렇게 지어봤다.
C는 multigraph 즉, 꼭짓점 사이 여러 변이 허용되는 그래프라고 하자. m은 모든 정점의 개수
i의 연결성 $k_{i}$ , j의 연결성$k_{j}$라고 하면 정점 i와 j 사이의 간선의 수의 기댓값은 $\frac{k_{i}k_{j}}{2m}$
내가 이해한 방식이 맞는 진 모르겠지만 , switching 방식으로 봤을 때 정점 i가 endpoint로 고를 수 있는 정점이 $k_{i}$개, 그리고 pair로 정점 j가 선택 될 확률이 전체 $\frac{1}{m}$이고 endpoint를 고르는 경우 $k_{j}$, 그리고 i 기준으로 j를 선택하는 것과 j 기준으로 i를 선택하는 것이 중복되니 2로 나눠줘 이런 기댓값이 나온다고 생각했다.
랜덤으로 만들어 낸 그래프와 현실에서의 그래프가 차이가 클 수록 현실이 더 유의미한 것을 의미하게 된다.

📌 군집 탐색 알고리즘
1. Girvan-newman 알고리즘
- 대표적인 하향식 군집탐색 알고리즘
- 군집들이 서로 분리되도록 간선들을 순차적으로 제거
- 매개 중심성 기준으로 간선 제거
- 알고리즘
1) 전체 그래프에서 시작한다.
2) 매개 중심성이 높은 순서로 간선을 제거하면서, 입력 그래프에서의 군집성을 변화를 기록한다.
3) 매개 중심성을 재계산하고, 모든 간선이 제거 될 때까지 2~3 을 반복한다.
4) 군집성이 가장 커지는 상황을 복원한다.
5) 이 때, 서로 연결된 정점들, 즉 연결 요소를 하나의 군집으로 간주한다.

군집과 군집 사이의 다리 역할을 하는 간선들을 차례대로 제거한다.
이런 간선은 군집의 크기가 작아질수록 애매해지는데 어떻게 구할까?
매개 중심성(Betweenness Centrality) 을 기준으로 매개 중심성이 높을 수록 다리역할에 가까우므로 삭제해준다.
매개 중심성은 네트워크 내의 해당 간선이 정점간의 최단 경로에 놓이는 횟수를 의미한다.
정점 i로부터 j로의 최단 경로의 수를 $\sigma_{i,j}$라고 하고 간선 (x,y)를 포함한 것을 $\sigma_{i,j}(x,y)$ 라고 한다.

A에서 H로의 최단 경로는 A-D-E-H가 될 것이고, 간선 (D,E)를 포함한다.
이런 식으로 왼쪽의 군집 내 정점에서 오른쪽 군집 내 정점으로 가는 최단 경로에는 간선(D,E)가 무조건 포함되므로
$\sigma(A,H)$ = 16이 된다.
간선 (F,G)를 지나는 최단 경로는 정점F로부터 G까지 밖에 없으므로 $\sigma(F,G)$ = 1이 된다.
간선을 얼마나 제거했냐에 따라서 군집의 입도가 달라지게 된다.

간선을 제거할 떄마다 계산한 군집성 중 군집성이 가장 최대가 되는 지점까지만! 간선을 제거해준다.
2. Louvain 알고리즘
- 대표적인 상향식 군집 탐색 알고리즘
- 개별 정점에서 시작해 점점 큰 군집 형성
- 알고리즘
1) Louvain 알고리즘은 개별 정점으로 구성된 크기 1의 군집들로부터 시작
2) 각 정점 𝑢를 기존 혹은 새로운 군집으로 이동. 이 때, 군집성이 최대화되도록 군집을 결정
3) 더 이상 군집성이 증가하지 않을 때까지 2)를 반복
4) 각 군집을 하나의 정점으로하는 군집 레벨의 그래프를 얻은 뒤 3)을 수행
5) 한 개의 정점이 남을 때까지 4)를 반복
왕 너무 어렵다. cs224w에서는 이를 2가지 과정으로 설명한다.
phase 1 : 정점 v에 대해서 자기 이웃 정점 u의 군집에 넣으면 발생하는 군집성을 계산한다.
이때 가장 큰 군집성이 계산된 군집으로 이동하게 된다.
이를 더 이상의 군집성이 변화하지 않을 때까지 반복한다.
이 과정을 "Modularity optimizatoin"이라고 한다.
이 후 하나의 군집을 하나의 supernode로 압축한다.
군집 사이에 간선이 연결되어있었다면 super node들끼리도 연결된다.
supernode들 사이의 간선의 가중치는 두 군집 사이 연결되었던 간선들의 가중치의 합이다.
"Community Aggregation"이라고 설명한다.

Modularity optimizatoin에 의해 첫번째 그래프가 두번째 그래프와 같이 군집을 형성하게 된다.
그리고 "Community Aggregation"에 의해 supernode들로 압축이 된다.
군집 내에서의 간선이 존재해, supernode의 간선이 자기 자신에서 시작해서 자기 자신으로 돌아오게 된다.
예를 들어 녹색 군집에서 보라색 군집사이의 연결된 간선은 (4,10) 하나 뿐으로 supernode의 가중치가 1이 된다.
보라색 군집은 0,1,2,4,5번 노드에 해당하는 연결성의 합인 14를 가중치로 가지게 된다.
phase 2는 phase1을 한 번 더 반복하는 과정이다.
supernode들에 대해 개별 군집으로 바라보고, 가장 큰 군집성이 계산되는 군집으로 이동하면서 더 이상의 군집성이 변화되지 않을 때까지 반복한다. 이후 또 supernode로 압축해준다.

📌 중첩이 있는 군집탐색
- 실제 그래프는 중첩되어있는 경우가 많음
- Girvan-Newman , Louvain 알고리즘은 군집 간의 중첩이 없다고 가정. 그러면 중첩되어 있는 군집은 어떻게 할까?

으아;; 여기 너무 어렵다. 강의랑 ppt만으로는 정말 해결이 안된다.
community affiliation graph model (AGM)이라는 그래프 생성 모델을 정의한 후,
그래프 G가 AGM에 의해 성성 되었다고 가정한다. 이때 G를 생성하는 가장 best한 AGM을 찾는다.

여기서의 community : 군집 , memberships : 소속관계 , nodes : 정점이다.
정점의 수, 간선의 수가 주어진 community affiliation model을 통해 그래프를 생성한다.
그래프를 생성한다는 건 무슨 뜻일까? 즉 edge를 디자인 한다는 거다.
정점과 군집이 정해져있으므로 간선의 수에 맞춰 점들을 연결해주는 것이다.
간선의 디자인에 따라 여러가지 network가 생성되고, 그 네트워크들이 각각 나올 확률을 그래프 확률이라고 이해했다.
각각의 군집들은$ P_{c} $라는 파라미터를 가진다.
하나의 군집 내 두 정점은 $P_{c}$의 확률로 직접 연결된다.
예를 들어 가운데 빨간 정점들 처럼 두 정점 다 여러 군집에 속하게 되면 어떡할까?
두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적이다.
이 때의 경우 두 정점이 간선으로 직접 연결될 확률은 $1 - (1-p_{A})(1-p_{B})$ 가 된다.
WHY? 이해 안돼서 30분동안 쳐다봤다. 근데 별 게 아니라서 실망했다.
두 정점이 두 집합 모두에 속한다면 군집A 관점에서 보든, 군집B 관점에서 보든 어쨌든 한 번 이상 연결이 되기만 하면 된다. 그래서 1 - (A에서 연결이 되지 않을 확룰)(B에서 연결이 되지 않을 확률) 는 3가지의 경우를 내포하고 있다.
: A에서 연결 & B에서 연결X , A에서 연결X & B에서 연결 , A에서 연결 & B에서 연결
이를 일반화하면 두 정점이 연결되어있을 경우는 아래와 같아진다.
c는 두 점이 속해있는 군집들을 얘기한다.

공통된 그룹의 수가 많아질수록1보다 작은 값들이 많이 곱해지기 때문에 뒷부분이 0에 가까워 전체적으로는 1에 가까워진다. 즉, 공통된 그룹의 수가 많을 수록 연결될 가능성이 커지는 것이다.
만약, 두 점이 파란점과 초록점처럼 공통으로 속하는 군집이 없다면 어떡할까? 이때는 0이 되는데, 이를 방지하기 위해 $\epsilon$ 엡실론으로 대체해준다.
반대로 graph로부터 model을 얻을 수도 있다.
그래프가 주어졌을 떄, 우리는 affiliation graph M과 군집의 수 C , 각 군집의 확률 Pc 모델의 파라미터 F를 찾아야한다.
Maximum likelihood Estimate 문제가 된다.
그래프 G가 주어졌을 때, 이 G를 가장 잘 설명할 수 있는 , 즉 파라미터가 최대가 되는 F를 찾아줘야된다.

gradient descent와 같은 최적화 기법을 통해 F가 학습되면서 결국 F가 만들어낸 P(u,v)와 G의 p(u,v)의 차이가 제일 작아지는 파라미터들을 찾을 수 있게 된다.

'Naver Ai Boostcamp' 카테고리의 다른 글
| [Day 24] 정점 표현 (0) | 2021.02.27 |
|---|---|
| [Day 23.5] 추천시스템 (기초 ~ 심화) (0) | 2021.02.26 |
| [Day 22] 페이지랭크 & 전파 모델 (0) | 2021.02.23 |
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
| [DAY 20] self-supervised pretrained model - Bert , GPT (0) | 2021.02.20 |