📌 학습목표
- 정점, 간선, 방향성, 가중치 등의 정의들을 명확하게 이해
- 실제 그래프의 다양한 패턴에 집중
📌 그래프 기초
- 그래프란?
그래프는 정점 집합과 간선집합으로 이루어진 수학적 구조를 얘기한다.
동그라미 혹은 점들을 정점이라 부르고, 그 점들을 잇는 선을 간선이라고 한다.
정점들의 집합을 V , 간선들의 집합을 E , 그래프를 G = (V,E)라고 적는다.
그래프는 네트워크 , 정점은 노드, 간선은 엣지 혹은 링크라고도 불린다.
두 정점을 간선으로 이어 두 정점이 연결됐다는 것을 나타낸다.
생각해보면 우리가 어렸을 때 그리던 "마인드맵"도 그래프다.

그래프는 크게 "방향의 유무", "가중치의 유무" ,"정점의 종류"등에 의해 구분된다.
여기서는 간단하게만 다루고, 알고리즘에서 사용되는 더 다양한 그래프의 종류에 대해선 이곳에서 잘 설명하고있다.
- 방향의 유무

방향이 없는 그래프는 페이스북 친구 그래프와 같이 A가 B와 친구라면 B와 A도 친구인 거와 같이 항상 양방향이다.
그렇기 때문에 이를 (A,B)라고 표현하면 (B,A)도 동일한 표현이 된다.
방향이 있는 그래프는 트위터 팔로우 그래프와 같이 A가 B를 팔로우했다고, B도 A를 팔로우하는 것은 아니다.
이렇게 간선에 방향성이 존재해 A->B로만 갈수 있는 간선은 <A,B>로 표시하고 이는 <B,A>와는 다르다.
- 가중치의 유무

가중치가 없는 그래프는 페이스북 친구 그래프같이 모든 정점이 동등한 위치?일 때, 표현된다.
가중치가 있는 그래프는 유사도 그래프와 같이 A,B,C 모두 유사하지만, 그 중 특히 A,B는 더 유사하고, B,C는 덜 유사하다와 같이 모든 정점이 동등한 위치가 아닐 때를 표현한다.
- 정점의 종류
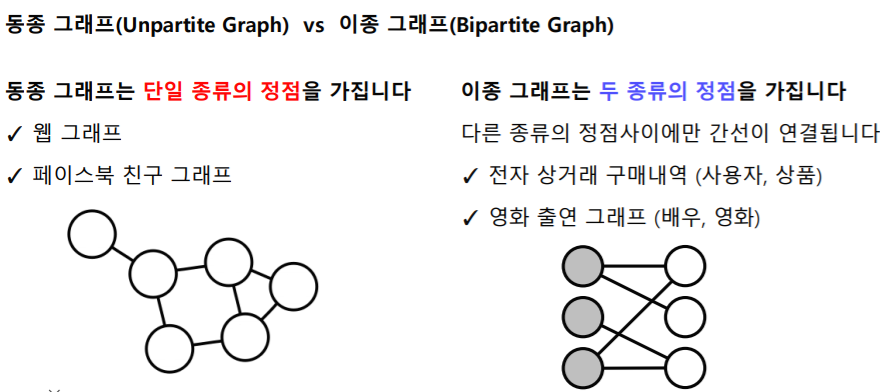
동종 그래프는 정점간의 종류가 같다. EX) 사람-사람
이종 그래프는 사용자 - 상품 처럼 정점간의 종류가 다른 그래프를 얘기한다.
사용자가 상품을 사기 때문에, 사용자와 상품 즉 다른 종류의 정점 사이에만 간선이 연결되고, 사용자-사용자, 상품-상품과 같이 같은 종류의 정점사이에는 간선이 연결되지 않는다.
그래프의 유형을 정의하는 것은 상당히 주관적인 일이다.
페이스북 친구 그래프이더라도 내가 만약 더 연락을 많이 한 사이에 가중치를 두고싶다면 가중치가 있는 그래프로 표현할 수도 있고, "연결됐다"에만 포커스를 둔다면 인스타 팔로우도 방향이 없는 그래프로 표현할 수도 있을 것이다.
즉, 그래프는 가지고 있는 데이터, 하고자 하는 분석의 목적에 따라 유형이 달라진다.
📌 그래프의 표현 방법
이런 그래프들을 일일히 그림으로 그리지 않고 컴퓨터가 이해하기 위해서는 어떻게 표현해야할까?
- 간선리스트 : 그래프를 간선들의 리스트로 저장
- 각 간선은 해당 간선이 연결하는 두 정점들의 순서쌍(pair)로 저장된다.
방향성이 있는 경우 아래와 같이 (출발점, 도착점) 순서로 저장해주고, 방향성이 없는 경우에는 순서에 대해 고려해주지 않는다.
잘은 모르겠지만,, 알고리즘을 이용해 그래프를 구현할 때, 간선리스트를 사용한 적은 거의 드문 거 같다.

- 인접 리스트 : 각각의 정점에 대해 인접한 정점 번호를 저장
방향성이 있는 경우와 방향성이 없는 경우 다르게 구현된다.

graph = [[2,5],[1,3,5],[2,4],[3,5,6],[1,2,4],[4]]
for i in range(len(graph)):
print(f"{i+1} : {graph[i]}")
# 1 : [2, 5]
# 2 : [1, 3, 5]
# 3 : [2, 4]
# 4 : [3, 5, 6]
# 5 : [1, 2, 4]
# 6 : [4]
가중치가 있는 그래프를 인접리스트로 구현할 떄는 주로 정점에서 나가는 노드들만 적어주는 것 같다.
graph = [[2],[5],[2,4],[5,6],[1,2],[]]
for i in range(len(graph)):
print(f"{i+1} : {graph[i]}")
# 1 : [2]
# 2 : [5]
# 3 : [2, 4]
# 4 : [5, 6]
# 5 : [1, 2]
# 6 : []
- 인접행렬
: 방향성이 있는 경우를 위주로 설명하면 정점 수를 v라고 할 때, $V \times V$크기의 2차원 matrix를 만들어준다.
정점 i 에서 j로의 간선이 있다면 i행 j열 원소를 True를 의미하는 1을 채워주고, 없다면 0을 채워준다.

graph = [(1,2) , (2,5) ,(3,2) , (3,4) , (4,3) , (4,5) , (4,6) , (5,1) , (5,2)]
matrix = [[0 for _ in range(6)]for _ in range(6)]
for i in range(6) :
for j in range(6):
if (i,j) in graph :
matrix[i][j] = 1
else :
matrix[i][j] = 0
for i in matrix : print(i)
# [0, 0, 0, 0, 0, 0]
# [0, 0, 1, 0, 0, 0]
# [0, 0, 0, 0, 0, 1]
# [0, 0, 1, 0, 1, 0]
# [0, 0, 0, 1, 0, 1]
# [0, 1, 1, 0, 0, 0]
📌그래프를 왜 사용할까?
세상은 수많은 복잡계(complex system)으로 이루어져있다.
친구관계, 정보와 지식, 심지어 우리의 신체까지도 복잡계로 이루어져있으며, 구성 요소간의 복잡한 상호작용을 한다.
이를 간단한 표현으로 단순화하고 분석하기 위해 "그래프"를 사용한다.
또 SNS 분석 시 관계, 상호작용 같은 가시적이지 않은 추상적인 개념을 시각화 하는 데 도움이 된다.
아래 이미지는 코로나 확진자의 이동경로를 그래프로 나타내 시각화 한 것이다.

위와 같은 복잡계를 이해하고, 정확한 예측을 하기 위해서는 이면에 있는 그래프에 대한 이해가 반드시 필요하다.
- 인공지능에 graph를 어떻게 적용할 수 있을까?
- 정점분류(Node classification) ex) 트위터에서의 공유 관계를 분석해, 각 사용자(정점)의 정치적 성향 파악
- 연결예측(Link prediction) ex) 페이스북 소셜네트워크가 어떻게 진화할까?
- 추천(Recommendation) ex) amazon의 사용자에게 필요한, 만족도가 높을 물건을 추천
- 군집분석 (clustring) ex) 연결관계로부터의 사회적 무리 (social circle)을 파악
- 랭킹 및 정보검색(information retrieval) ex) 웹이라는 그래프에서 중요한 웹페이지 파악, 선정
- 정보전파(information cascading) 및 바이럴 마케팅(viral marketing)
📌 그래프 라이브러리 NetworkX
파이썬 라이브러리로, 그래프를 생성, 변경, 시각화 할 수 있으며 구조와 변화 역시 살펴 볼 수 있다.
# 실습에 필요한 library를 임포트합니다.
import networkx as nx # NetworkX
import numpy as np # 선형대수를 위한 라이브러리
import matplotlib.pyplot as plt
import sys
# 그림을 그리기 위한 라이브러리
np.set_printoptions(threshold=sys.maxsize)
G= nx.Graph() # 방향성이 없는 그래프 : Graph
DiGraph = nx.DiGraph() # 방향성이 있는 그래프 : DiGraph
for i in range (1, 11):
G.add_node(i)
print("Num of nodes in G : " + str(G.number_of_nodes())) # 정점의 수 반환 : number_of_nodes
print("Graph : " + str(G.nodes)+ "\n") # 정점의 목록 반환 : nodes
# Num of nodes in G : 10
# Graph : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
for i in range (2, 11): # 간선 추가
G.add_edge(1, i)
print("Graph : " + str(G.edges) + "\n") # 간선의 목록 반환
# Graph : [(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9), (1, 10)]
# 그래프를 시각화
# 정점의 위치 결정 (상당히 중요)
pos = nx.spring_layout(G)
# 정점의 색과 크기를 지정하여 출력
im = nx.draw_networkx_nodes(G, pos, node_color="red", node_size=100)
# 간선 출력
nx.draw_networkx_edges(G, pos)
# 각 정점의 라벨을 출력
nx.draw_networkx_labels(G, pos, font_size=10, font_color="black")
plt.show()
그래프 저장방식도 인접리스트, 간선리스트, 인접행렬로 나뉘는데 인접행렬은 일반행렬과 희소행렬로 나뉜다.
- 간선리스트로 저장
# 그래프를 간선 리스트로 저장
print("###### Graph to EdgeList ######")
EdgeListGraph = nx.to_edgelist(G) # to_edgelist : 간선리스트
for e in EdgeListGraph:
v1, v2, w = e # 시작노드, 도착노드, 가중치로 구성
print(v1, v2)
###### Graph to EdgeList ######
#[(1, 2, {}), (1, 10, {}), (2, 3, {}), (3, 4, {}), (4, 5, {}), (5, 6, {}), (6, 7, {}), (7, 8, {}), (8, 9, {}), (9, 10, {})]
#1 2
#1 10
#2 3
#3 4
#4 5
#5 6
#6 7
#7 8
#8 9
#9 10- 인접리스트로 저장
# 그래프를 인접 리스트로 저장
print("###### Graph to List ######")
ListGraph = nx.to_dict_of_lists(G) #인접리스트 : to_dict_of_lists
for v in DictGraph:
print(str(v) + " : " + str(ListGraph[v]))
###### Graph to List ######
# 1 : [2, 10]
# 2 : [1, 3]
# 3 : [2, 4]
# 4 : [3, 5]
# 5 : [4, 6]
# 6 : [5, 7]
# 7 : [6, 8]
# 8 : [7, 9]
# 9 : [8, 10]
# 10 : [9, 1]- 인접행렬(일반행렬) 저장
: 일반행렬은 전체 원소를 저장해, 정점수의 제곱에 비례하는 저장공간을 사용하게 된다.
연결이 많이 되어있지 않아, 거의 주로 0으로 채워져있는 경우 비효율적이다.
# 그래프를 인접 행렬(일반 행렬)로 저장
print("###### Graph to numpy array ######")
NumpyArrayGraph = nx.to_numpy_array(G) #to_numpy_array : 인접행렬
print(NumpyArrayGraph)
###### Graph to numpy array ######
#[[0. 1. 0. 0. 0. 0. 0. 0. 0. 1.]
# [1. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
# [0. 1. 0. 1. 0. 0. 0. 0. 0. 0.]
# [0. 0. 1. 0. 1. 0. 0. 0. 0. 0.]
# [0. 0. 0. 1. 0. 1. 0. 0. 0. 0.]
# [0. 0. 0. 0. 1. 0. 1. 0. 0. 0.]
# [0. 0. 0. 0. 0. 1. 0. 1. 0. 0.]
# [0. 0. 0. 0. 0. 0. 1. 0. 1. 0.]
# [0. 0. 0. 0. 0. 0. 0. 1. 0. 1.]
# [1. 0. 0. 0. 0. 0. 0. 0. 1. 0.]]- 인접행렬(희소 행렬) 저장
: 0이 아닌 원소만을 저장해, 간선의 수에 비례하는 저장공간을 사용하게 된다.
일반행렬에서 0이 많은 경우 저장공간의 사용이 비효율적이었다.
이 때, 희소행렬을 사용하게 되면 훨씬 빠르고 효율적으로 사용할 수 있다.
# 그래프를 인접 행렬(희소 행렬)로 저장
print("###### Graph to Spicy sparse matrix ######")
SparseMatrixGraph = nx.to_scipy_sparse_matrix(G) # to_scipy_sparse_matrix:희소
print(SparseMatrixGraph)
###### Graph to Spicy sparse matrix ######
# (0, 1) 1
# (0, 9) 1
# (1, 0) 1
# (1, 2) 1
# (2, 1) 1
# (2, 3) 1
# (3, 2) 1
# (3, 4) 1
# (4, 3) 1
# (4, 5) 1
# (5, 4) 1
# (5, 6) 1
# (6, 5) 1
# (6, 7) 1
# (7, 6) 1
# (7, 8) 1
# (8, 7) 1
# (8, 9) 1
# (9, 0) 1
# (9, 8) 1
📌 실제 그래프는 어떤 특징을 가질까?
실제 그래프는 소셜네트워크, 전자 상거래 구매내역, 인터넷 등 다양한 복잡계 (complex system)으로부터 얻어진 그래프를 의미한다. 본 설명에서는 실제 그래프의 에시로 MSN메신저 그래프를 사용한다.
사람은 뭐든 비교대상이 있어야 특징이 더 확실해보인다.
실제 그래프와 랜덤 그래프를 비교해 실제 그래프의 패턴과 특징을 알아본다.
- 에르되스-레니 랜덤 그래프
랜덤 그래프란 확률적 과정을 통해 생성한 그래프를 의미한다. 즉, 특정한 확률분포에 따라 생성된 그래프를 얘기한다.
에르되스-레니 랜덤그래프는 임의의 두 정점 사이에 간선이 존재하는지의 여부를 확률분포에 의해 결정한다.
n개의 정점을 가질 때, 임의의 두 개의 정점 사이에 간선이 존재할 확률을 p라고 한다.
이 때 iid를 따르므로 정점간의 연결은 서로 독립적이어야한다.
위 조건을 만족하는 에르되스-레니 랜덤 그래프를 G(n,p)로 표기한다.
G(3, 0.3)에 의해 생성될 수 있는 그래프와 각각의 확률은 아래와 같다.
간선이 하나 생길 확률은 0.3이고, 생길 수 있는 간선의 개수는 $_{n}\textrm{C}_{2}$로 총 3개이다.
간선의 유무에 따라서 만들 수 있는 그래프의 개수는 $2^{3}$개가 된다.
각각의 그래프는 이항분포를 따라 존재할 확률이 결정된다.

📌 작은 세상 효과
- 경로
: 정점 𝑢와 𝑣의 사이의 경로(Path)는 아래 조건을 만족하는 정점들의 순열(Sequence)
- u에서 시작해서 v에서 끝남
- 순열에서 연속된 정점은 간선으로 연결되어있어야함
- [1,4,3,4,6,8]은 path지만 [1,6,8]은 연속된 정점 1,6이 간선으로 연결되어있지 않기때문에 path가 아님

- 거리
: u와 v 사이의 최단 경로의 길이로 path 내 간선의 수를 의미한다.
ex) 1과 8 사이의 최단경로는 1,4,6,8로 거리는 3이 된다. - 지름
: 정점 간 거리의 최댓값
2와 8 사이의 최단 경로는 [2,3,4,5,8]로 거리는 4다.
그래프 내에서 모든 정점간의 거리를 구했을 때, 2에서 8로 가는 거리 4가 최대이므로 이 그래프의 지름은 4가 된다.
- 작은 세상 효과
: 몇 가닥의 무작위 연결만으로도 모든 사람이 연결되는 걸 "작은 세상 효과"라고 한다.
케빈 베이컨의 6단계법칙과 같이 평균 6단계를 걸치면 지구상 대부분의 사람과 연결될 수 있다는 거다.- 실제 그래프의 큰 특징이다.
- 랜덤 그래프에서도 높은 확률로 나타나지만 , 항상 존재하는 것은 아니다.
아래와 같은 랜덤 그래프에서는 존재하지 않는다.

📌 연결성의 두터운 꼬리 분포
- 연결성 : 정점과 연결된 간선의 수를 의미한다.
해당 정점의 이웃들의 수와도 같다.

- 두터운 꼬리 분포
: 지수함수와 모양은 유사하지만, 지수함수보다 느리게 감쇠돼 꼬리부분이 두터운 분포

- 연결성의 두터운 꼬리 분포
: 실제 그래프의 연결성 분포는 두터운 꼬리분포를 가진다.- 연결성이 매우 높은 즉, 연결된 이웃들이 많은 허브 정점이 존재한다는 뜻이다.
- 허브정점은 평균을 훠얼씬 뛰어넘는 많은 수의 이웃들과 연결된 노드를 얘기한다.
- 현실 그래프에서는 교수님과 같이 연결성이 적은 정점들이 대부분이고, 연결성이 높은 방탄소년단과 같은 허브 정점들이 두터운 꼬리 부분에 존재한다.
- 랜덤 그래프의 연결성 분포는 높은 확률로 정규분포와 유사해 허브정점이 존재할 가능성은 0에 가깝다.

📌 거대 연결 요소
- 연결 요소
1) 연결 요소에 속하는 정점들은 경로로 연결될 수 없다.
2) (1)의 조건을 만족하면서 정점을 추가할 수 없다.
위 두 가지 조건을 모두 만족시키는 정점들의 집합을 연결요소라고 한다.- {1,2,3,4,5} , {6,7,8} , {9}라는 3개의 연결 요소가 존재한다.
- {1,2,3,4}는 1)은 만족하지만 , 1)을 만족하면서 5를 추가할 수 있기 때문에 연결요소가 아니다.

- 실제 그래프에는 대다수의 정점을 포함하는 거대연결요소가 존재한다.

- 랜덤 그래프에도 높은 확률로 거대연결요소가 존재한다.
- 단, 정점들의 평균 연결성이 1보다 충분히 커야한다.

📌 군집 구조
- 군집 : 정점 사이 많은 간선이 존재하고, 집합 외와는 적은 수의 간선이 존재하는 집합
- 아래 그림은 11개의 군집이 존재하고, 군집 내에는 셀수 없이 많은 간선이 존재하지만, 군집 끼리의 간선은 상대적으로 훨씬 적은 걸 확인 할 수 있다.

- 지역적 군집 계수
- 한 정점에서의 군집의 형성 정도를 측정
- 정점 i의 지역적 군집 계수는 정점 i의 이웃쌍 중 간선으로 직접 연결된 것의 비율로 $C_{i}$로 표현한다.
- 지역적 군집 계수가 높다는 건 이웃들이 높은 확률로 연결되어있단 뜻으로 높은 확률로 군집을 형성한다.

정점 1을 기준으로 연결되어있는 정점 즉, 이웃은 2,3,4,5로 총 4개가 존재한다.
그리고 만들 수 있는 이웃쌍은 (2,3) , (2,4) ,(2,5) ,(3,4) ,(3,5) ,(4,5) $_{4}C_{2}$로 총 6개가 존재한다.
그 중 3개 (2,4), (2,3) , (3,5)가 직접 연결되어있다.
따라서 $C_{1}$은 3/6으로 0.5가 된다.
분모가 되는 이웃쌍이 존재하지 않는 경우, 즉 연결성이 0인 정점과 1인 정점은 생각하지 않는다.
- 전역 군집 계수
- 전체 그래프에서 군집의 형성 정도를 측정
- 각 정점에서의 지역적 군집계수의 평균
- 예를 들어 위의 그래프에서 전역군집계수는 $C_{1}$ ~ $C_{5}$의 평균
- 실제 그래프에서는 군집계수가 높다. 즉 ,많은 군집 존재
- 동질성 : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높다.
- 대학에서 나잇대, 관심사, 성별이 비슷하면 하나의 무리를 만드는 것과 같은 얘기 - 전이성 : 공통 이웃이 매개역할을 한다.
- 내 친구야 서로 인사해~ 하면서 서로를 소개해주는 경우
- 동질성 : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높다.
- 랜덤 그래프에서는 지역적 혹은 군집계수가 높지 않다.
- 왜? 간선 연결이 독립적이기 때문에, 공통이웃의 존재 여부가 간선 연결 확률에 영향 X
- 즉, 실제 그래프에서는 간선 연결이 독립적이지 않음. 내 주변이 거의 다 이어져있을 확률이 큼.
하지만 랜덤 그래프는 독립적이므로, 내 주변과 상관없음
📌 그래프 별 비교하기

## 전역군집계수 계산
def getGraphAverageClusteringCoefficient(Graph):
ccs = []
for v in Graph.nodes: # 정점들을 list로 반환
num_connected_pairs = 0
for neighbor1 in Graph.neighbors(v): # 정점 v의 이웃 정점들
for neighbor2 in Graph.neighbors(v): # 이웃 정점들끼리 서로 이어진 것을 확인하기 위해 2중 for문
if neighbor1 <= neighbor2: # nC2를 구현하기 위해 한가지 경우는 무시해줌
continue
if Graph.has_edge(neighbor1, neighbor2):
num_connected_pairs = num_connected_pairs + 1
cc = num_connected_pairs / (Graph.degree(v) * (Graph.degree(v) - 1) / 2) # 실제 연결된 이웃쌍의 개수 / nC2: 가능한 모든 이웃쌍의 개수
ccs.append(cc)
return sum(ccs) / len(ccs)
## 지름 계산
def getGraphDiameter(Graph):
diameter = 0 # 알고리즘을 시작하기 앞서 diameter 값을 0으로 초기화합니다.
for v in Graph.nodes: # 그래프의 모든 점점들 대해서 아래와 같은 반복문을 수행합니다.
length = nx.single_source_shortest_path_length(Graph, v) # 1. 정점 v로 부터 다른 모든 정점으로 shortest path length를 찾습니다.
max_length = max(length.values()) # 2. 그리고 shortest path length 중 최댓값을 구합니다.
if max_length > diameter: # 3. 2에서 구한 값이 diameter보다 크다면 diameter를 그 값으로 업데이트 합니다.
diameter = max_length
return diameter # 반복문을 돌고 나온 diameter를 return합니
피어세션
질의응답 시간에는 재밌는 질문이나 얘깃거리가 나오진 않았다. 사실 잘 기억 안남
이번 주까지 각자 맡았던 걸 하나씩 구현해와서 공유했다.
- 보윤님 - freezing
: freezing 은 parameter들 list를 불러와 내가 고정하고싶은 부분만큼만 required_grad = False를 주면 된다.
옛날에 한 번 해봤었는데, freezing을 하는 이유가 pretrained 모델을 불러와 feature extract하는 부분은 큰 차이가 없으니 뒷 부분만 finetunning 하는 걸로 알고있는데, 어느 layer까지 얼리는 게 베스트냐,,,!가 문제같다. - 성훈님 - KFOLD
: 성훈님은 ImageFolder로는 kfold를 못할 거 같다 판단하셔서 customdataset을 따로 만들고 싸이킷런에서 KFOLD를 불러와 사진들의 이름이 담긴 리스트의 인덱스를 FOLD 시켰다. 말을 내가 너무 어렵게했네 Hmm,,
만약 K=5면 반복문을 5번씩 돌면서 바꿔줘야될 줄 알았는데, Kfold.split을 쓰면 자동으로 된다고 한다.
for train_index, test_index in kfold.split(features):- 보현님 - KFOLD
: 보현님은 imagefolder로 kfold를 구현해오셨다,,,! ImageFolder로 전체 이미지를 담고 Kfold로 나눠준 후, torch의 Subset이라는 기능을 사용해 나누어주었다.
dataset = torch.utils.data.Subset(dataset, indices[:-50])- 혜린님 - mixup
: 내가 봤을 땐 레드벨벳 멤버 얼굴이 다 거기서 거기여서 mixup을 쓰면 성능이 더 좋아질 거라 생각했다.
구현하고 느낀 점은 ,mixup은 잘 정제된 데이터에 적용해야 한다는 것,,,,
크롤링으로 모은 데이터셋을 최대한 전처리하긴 했지만,,, 노가다로 하지 않는 이상 모두 다 얼굴만 나오진 않는다.
목 + 얼굴이 합쳐진 괴이한 모양이 나온다.
def mixup_data(x, y, alpha=1.0):
'''Returns mixed inputs, pairs of targets, and lambda'''
if alpha > 0:
lam = np.random.beta(alpha, alpha)
else:
lam = 1
batch_size = x.size()[0]
index = torch.randperm(batch_size).to(device)
mixed_x = lam * x + (1 - lam) * x[index, :]
y_a, y_b = y, y[index]괴이한 모양을 보고싶다면 아래 더보기를 누르시면 보입니다... 새벽에 보는 거 추천하지 않아요
- 보현님의 질문 : no_grad()
보현님은 항상 반짝반짝한 눈으로 좋은 질문들을 많이 해주신다.✨👀
eval()을 선언해놓고 torch.no_grad()를 하는 이유는 그렇게 하면 autograd를 꺼 메모리 사용량을 줄이고 연산속도를 높힐 수 있다.
더 자세한 얘기는 해당 링크에 들어가서 읽어보시길
오늘 뭔가 수업이 재미가 없다. 요새 그렇게 핫하다는 GNN? Collaborative filtering? 기대했는데 재미가 없다.
내일은 재미있겠지? 기대 중 👀
'Naver Ai Boostcamp' 카테고리의 다른 글
| [Day 23] 군집 탐색 (0) | 2021.02.24 |
|---|---|
| [Day 22] 페이지랭크 & 전파 모델 (0) | 2021.02.23 |
| [DAY 20] self-supervised pretrained model - Bert , GPT (0) | 2021.02.20 |
| [DAY 19] Transformer (0) | 2021.02.18 |
| [DAY 18] Seq2seq , beam search , BLEU (1) | 2021.02.17 |
