14일차 최성준 교수님의 강의 + 19일차 주재걸 교수님의 강의를 듣고 학습정리한 내용입니다.
Transformer
90년대 이전 생이라면 가족오락관의 <고요속의 외침>을 한번씩 봤을 거다.
어떤 단어를 외쳐서 뒷사람에게 넘기고 넘기고 넘겨서 그 단어가 뭔지 마지막 사람이 맞추는 게임이다.
첫 번째 사람이 말한 단어가 점점 뒤로 갈수록 이상한 단어가 되곤 한다.
"미꾸라지"로 시작된 단어가 "비누다시"가 되는 놀라운 기적을 엿볼 수 있다.

Seq2seq가 딱 이렇다. 물론 귀를 막진 않고 정확한 정보를 넘겨주긴 하지만 길면 길어질수록 첫 번째 단어에 대한 정보를 점점 잃어간다. 우린 이런 문제를 "Long term dependency"라고 한다. RNN을 사용하면 attention 을 추가하고, LSTM으로 바꿔도 순차적으로 학습해야하기 때문에 어쩔 수 없이 생기는 문제인 거 같다.
Transformer는 self-attention을 이용해 RNN을 사용하지않고 encoder, decoder를 만들어 기존의 문제점들을 해결했다.2017 NIPS에서 Google이 transformer를 발표해 큰 주목을 이끌고 이후 많은 것들이 변했다.요새는 Vit 등 transformer를 이용해 vision문제를 풀기도 한다. 여러 분야에서 사용되기 때문에 모든 조교님 및 교수님들이 이건 꼭 알고 넘어가야된다!! 라고 엄청난 강조를 하신다.
- n개의 단어가 어떻게 한 번에 처리되는지
- 인코더에서 디코더로 어떤 정보를 넘겨주는지
- 디코더가 어떻게 그에 맞는 문장을 출력하는지
최성준 교수님께서 이렇게 3개만 중점적으로 이해해도 아주 큰 성과라고 하셨다.
먼저 transformer에 제일 큰 기여를 한 self attention에 대해 알아보자.
📌 Self-Attention
-
Self attention

self-attention은 이 논문에서 처음 등장한 개념으로 이전에 나왔던 attention들과는 달리 Query , Key , Value를 자신으로부터 구한다. 세 값이 모두 같다는 뜻이 아니라 출처..? 근본...?이 같다는 뜻이다.
단어의 임베딩 값에 Q,K,V 별 가중치를 곱해 각 단어에 해당하는 Query , Key , Value 벡터를 만들어낸다.
내가 이해한 Q,K,V에 대해서는 어제도 얘기했지만 이렇게 생각한다.
Q : 질문
K : 질문에 대한 답
V : 답의 점수다.
x1, x2, x3가 input으로 한 번에 들어온다.
x1에 $W^{Q}$를 곱해 q1을 만들어준다. (=seq2seq에서는 decoder의 hidden state에 해당)
q1은 누가 "I"와 유사하니?라는 질문 역할을 한다.
input으로 들어온 모든 x1,x2,x3에 대해 $W^{K}$를 곱해줘 각각의 키벡터 k1, k2,k3를 만들고 이를 q1과 내적해준다.
그러면 "I"라는 단어에 대해 각각의 "I" , "go" , "home" 단어들과 유사도가 계산된다.
이렇게 각각 q1-k1 , q2-k2 , q3-k3에 해당하는 attention score로 이뤄진 벡터를 만들 수 있고, 이를 softmax를 취해 0과 1 사이의 값으로 만들어준다.
input으로 들어온 모든 x1,x2,x3에 대해 $W^{V}$를 곱해줘 각각의 키벡터 v1, v2,v3를 만들고, 이전에 구한 attention score를 해당하는 키벡터와 dot production을 통해 attention output을 구해줄 수 있다.
seq2seq에서는 key, value 모두 encoder의 hidden state들로 같았지만 self attention에서는 서로 다른 Wk, Wv를 곱해줘 다른 값이 된다.
그렇게 만들어진 h1은 q1에 해당하는 "I"와 나머지 단어 "I" , "go" , "home"의 관계를 계산한 벡터이다.
각각의 쿼리 Q에 대해 위와 같이 하나하나 진행하지 않고 Transformer에서는 matrix 하나로 계산을 끝내버린다.

하나의 matrix로 attention계산을 하게 되면 attention output을 구하는 과정을 하나의 수식으로 표현할 수 있게 된다.

갑자기 $\sqrt{d_{k}}$로 나누는 것에 대해선 아래에서 설명한다.
Q와 K는 서로 내적되어야 하므로 동일한 차원 $d_{k}$를 가져야 한다.
V는 Q,K의 차원과는 상관없지만 실제 코드로 구현시에는 통일감을 주기위해(귀찮아서) 같은 차원으로 맞추는 경우가 많다고 한다.

Q와 K가 내적해 만들어진 행렬의 각 행은 쿼리벡터를 의미한다.
Q1 가 "I"를 의미한다면 Q와 K가 내적해 만들어진 행렬의 첫번째 행은 "I"와 다른 단어간의 유사도를 의미한다.
그 후 V와 곱해지는데 attention output의 한 행은 결국 attention score가 각 행렬 V에 row-wise하게 곱해진 값을 더한 값, 즉 weighted sum을 의미한다.
각 행별로 0.1, 0.2, 0.3, 0.4를 각각 곱해 더한 값이 attention output의 첫번째 행이 된다.
-
Scaled Dot Production
정확히는 $QK^{T}$에 softmax가 취해지는 게 아니라 이를 쿼리 벡터의 길이로 scale한 값에 softmax가 취해지게 된다.
이를 scaled dot production이라고 한다.
우리는 Q와 K에 해당하는 값들이 모두 평균 0 , 표준편차가 1인 가우시안 분포를 따른다고 가정한다.
$QK^{T}$의 평균은 0 이지만 분산은 Q와 V의 차원의 길이인 $d_{k}$가 된다.
즉 차원이 커질수록 분산도 차원만큼 커지게 된다.분산이 커지면 왜 안좋을까?
분산이 커지면 softmax를 취했을 때 편향이 심해진다.
차원이 4일 때와 100일때를 비교해보자. 차원이 4일때는 표준편차가 2가 된다. (위의 손그림이라고 가정)$QK^{T}$의 첫번째 행만 한 번 봐보면 [- 1.8 , 0.5, 2, 0] 나올 수 있다. 나름 골고루 분포된? 분포의 가장 오른쪽에 위치값과 가장 왼쪽에 위치한 값,가운데 값 등을 고려해서 고른 숫자들이다 ㅎㅎsoftmax를 취하게 되면 [0.016 , 0.16 , 0.72 , 0.09] 가 나오게 된다.
차원이 100일 때는 표준편차가 10이 되고 위와 똑같이 고려해 숫자를 뽑았을 때, $QK^{T}$의 첫번째 행만 한 번 봐보면 [- 9 , 0.5, 0, 10] 나올 수 있다.이때 softmax를 취하게 되면 [5.6e-9 , 7e-5, 4e-5, 0.999]와 같이 엄청나게 치우쳐져있는 즉 마지막 10에만 모든 몰빵되어있는 값이 나올 수 있게 된다.
이런 경우 softmax가 very peaked라고 표현하고 이는 gradeint를 작게 만들어 grdient vanishing문제를 불러일으킨다.그렇기 때문에 $QK^{T}$를 $d_{k}$로 나누어주어 표준편차가 1이 될 수 있도록 해준다.스케일링을 통해 더 안정적인 gradient를 가지게 된다고 한다. 본 논문에서는 $d_{k}$=8로 설정해두고 있다.
scaled dot product self attention을 사진 한장으로 정리해보면 이렇다!

📌 Multi-head attention
Multi head attention은 "협업"과 비슷하다.
혼자서는 한가지밖에 생각밖에 못하니 토론,팀플 등의 협업을 통해 여러 사람들과 함께 고민해 더 많은 생각을 해서 더 좋은 결과를 내는 것이다.
예를 들어 "I"와 관련해 head1은 주어의 위치를 보고, head2는 동사와의 관계를 보고, head3은 주어를 누가 꾸미는지를 보는 등 각자 다른 거에 집중해서 더 좋은 결과를 가져온다.

논문에서의 설명과 실제 코드를 구현할 때 좀 다르게 multi head를 구성한다.
논문에서는 Q,K,V를 512차원 , head =8이라 설정하고 512차원짜리 Q,K,V를 8개씩 잘라 총 64차원의 head8개를 만든다.
하지만 이외 구현이나 설명등에서는 $W^{Q}$의 경우 512차원을 가지는데 이를 8개로 잘라 각각 64차원짜리의 $W^{Q}_{i}$를 8개 만들었다.
$W^{Q}$뿐만이 아니라 $W^{K} , W^{K}$에 대해서도 똑같이 진행한다.
차이는 논문에서는 W는 512로 곱해진 Q,K,V를 8개로 나누었다면 , 실제 구현에서는 가중치 W를 8개로 나눈다.
어차피 Head에서의 차원이 감소하기 때문에 cost는 full dimension일때의 sinlge attention이나 multi head나 똑같다.
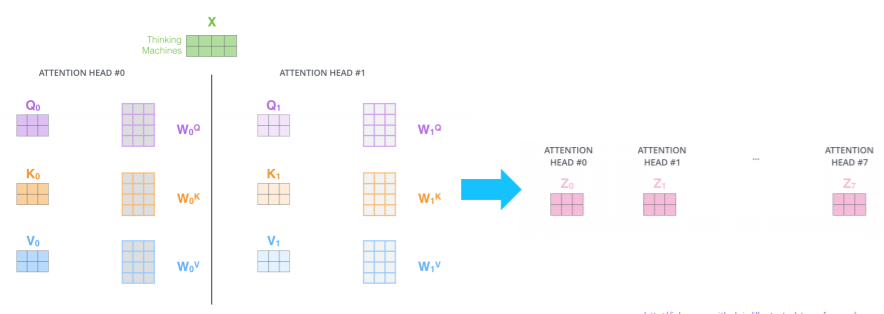
Multi-head self attention 을 보면 self attention 계산 과정을 서로 다른 8개의 weigt행렬들을 병렬로 곱해준 후 concatenate해준다. 이후 input의 차원과 맞춰주기 위해 가중치행렬을 곱해준다.

아래 그림에서 주황색 head self attention은 it을 the animal과 연관있다고 본다.
하지만 초록색은 it을 tired가 가장 연관이 있다고 본다.
이런 식으로 multi head attention은 표현력을 더 확장시켜주는 역할을 한다.

📌 Transformer
이제 본격적으로 transformer를 살펴보자. 이제서야 본격적이라니,,,ㅜㅜ
transformer는 rnn 없이 오로지 attention mechanism만을 사용한 구조다.
크게 봤을 때 encoder, decoder가 총 6개가 쌓여있고, 모델 구조나 input shape의 정보등은 다 같지만 가중치는 레이어들끼리 공유하지 않고 각자 다르다.
encoder는 Multi-Head self Attention과 feed forward network인 2개의 sub layer로 이루어져있다.
decoder는 Masked Multi-Head self Attention , Multi-Head Attention과 feed forward network 총 3개의 layer로 이루어져있다.
맨 마지막에는 linear + softmax를 거쳐 output probabilities를 출력하게 된다.
encoder부터 살펴보자.

📌 Encoder

-
Positional Encoding
transformer는 rnn처럼 순차적으로 정보를 주지 않기때문에 위치정보를 고려하지 못한다.
위치정보를 고려하지 못한다면 한 문장 내 단어들이 중복되어 나올 때 같은 단어로 인식한다.
이 부분을 보완하기 위해 positional encoding을 input embedding에 더해준다.

이렇게 되면 만약 같은 단어라 word embedding은 같더라도, 서로 다른 positional encoding값을 더해주기 때문에 각자 다른 벡터를 가지게 돼 순서정보가 고려된다.

이 식에서 pos는 입력문장 내 벡터의 위치를 나타내고, i는 한 단어의 임베딩 벡터 내에서 차원의 인덱스를 의미한다.
sin,cos으로 이루어져 -1 ~ 1 사이의 값이기 때문에 테스트 시 학습할 때 보지못한 더 긴 문장이 들어와도 문제 없이 positional encoding을 잘 해낸다.
-
Multi-Head self Attention
input embedding 혹은 이전 encodeer layer로부터 넘어온 input vector들에 대해 각각의 Q,K,V 가중들을 곱한 값들이 Multi-Head self Attention의 Q,K,V가 된다. 즉 Q,K,V 모두 하나의 encoder 내에서 주어지므로 self-attention이 가능케 된다. 이 과정에 대해서는 위에서 설명했으니 길게 말하지 않겠다
-
Add & Normalize
Resnet에서 나온 skip connection 개념을 사용한다.
attention을 거쳐 나온 값과 input embedding값을 더해 정보를 더 잘 보존해준다.
이후 layer normalization을 해준다.
하나의 batch 내에서 모든 feature들에 대해 평균0 , 분산1로 normalizaion을 해주는 거다.
batch와의 차이점은 아래와 같다.

normalizaion은 두가지 step으로 이루어져있는데 우선 각각 평균0, 표준편차1이 되게 normalize를 해준다.
그 후 각각 학습 가능한 가중치를 통해 affine transformaion을 해준다.

-
Position-wise Feed-Forward Networks
두 개의 linear transformation 사이에 RELU activate함수가 들어간다.
즉 , linear transformation을 한 후 relu를 하고 다시 linear transformation한다는 뜻이다.

레이어끼리는 서로 다른 parameter를 쓰지만., 한 layer에서 만큼은 서로 다른 position이더라도 같은 linear transformation (w1, w2, b1, b2)를 사용한다.
맨 위의 그림에서 z1, z2가 각각 FFNN을 거치는 것을 볼 수 있는데 모두 같은 W1, W2를 사용한다는 뜻이다.
📌 Decoder
이제 decoder 차례다.
encoder와 동일하게 위치정보를 나타내주는 positional encoding 과정을 거쳐야한다.
-
Masked Multi-Head self Attention
encoder와는 비슷한 듯 약간은 다른데 decoder에서는 번역을 해주어야한다.
trian 시에는 번역문장의 ground truth를 알지만 inference 시에는 알지 못한다.
현재 input으로 들어온 토큰 이후의 정보들에 대해서는 몰라야 되는 것이다.
즉 "i go home"을 "나는 집에 간다"라고 번역 해야 하는 경우 input으로 들어온 <sos>토큰은 자기 자신만 참고해서 만들어 "나는"을 만들어내야하고, 다시 "나는"이 input으로 들어오면 <sos>토큰과 "나는"만을 고려해야된다.
그렇기 때문에 쿼리에 해당하는 단어와 같은 단어 이후에 나오는 단어의 K는 고려하지 않는다.

학습 시 디코더는 정답에 해당하는 문장 행렬을 알고있기 때문에 현재 시점의 단어를 예측하려할 때, 미래의 단어까지도 참고하는 문제가 생긴다. 이 점을 해결하기 위해 Masked self attention은 현재 시점의 예측에서 미래를 참고하지 못하게 하려고 미래의 단어들을 다 마스킹해버린다.

-
Multi-Head Attention
이 곳에서의 attention은 이전의 self attention과는 다르다.
encoder layer의 가장 마지막에 위치한 encoder의 output은 K,V로 변형이 돼 decoder에 넘겨지게 된다.

이후 decoder에서 이전과 동일하게 multi head attention을 진행해준다.
query는 decoder에서 오고, k,v는 encoder에서 오므로 self 가 아닌 그냥 attention이다.
이를 "encoder -decoder attention"이라고도 한다.

📌 linear + softmax layer
decoder의 마지막 layer의 output를 vocab size에 맞추기 위해 Linear 즉 Fully connected layer를 한 번 거치게 된다. 이후 softmax를 한 번 더 거쳐 모두 0~1 사이의 확률값으로 표현되고, 이 중 가장 큰 값의 인덱스에 해당하는 word를 최종 output으로 출력하게 된다.

📌그 외
- transformer에서는 label smoothing 기법을 사용했다.
- warm up learning rate scheduler
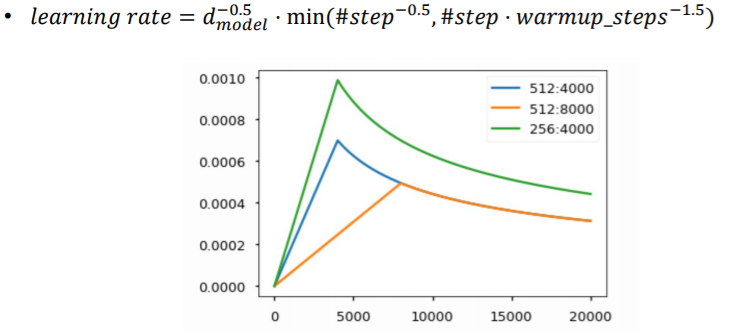
학습 초기에는 gradint가 너무 크기 때문에 적은 학습률에서 시작하다가,
어느 정도 완만한 구간 혹은 local minimum에서 탈출하기 위해 큰 학습률을 사용했다가.
global minimum근처에 간 경우 조금 더 섬세하게 움직여야 하기에 학습률을 점점 낮췄다.
📌 rnn과의 복잡도 비교

이걸 반년동안 이해를 못했는데 오늘로서야 비로소 이해가 됐다.
-
self attention
- complexity per layer
: self attention에서 Q와 K의 내적을 통해 (n x d) x (d x n) 행렬이 곱해진다.
Q의 한 row 당 연산이 dxn번 된다는 얘기고, 그런 row 가 총 n개 있으므로 complexity per layer는 $O(n^{2} \cdot d)$가 된다. - sequential opeations & maximum path length
: gpu가 뒷받침만 된다면 행렬이므로 여러 gpu를 써서 한 번에 계산할 수 있다.
또 rnn처럼 1번째 word에 가려면 n번을 돌아가야 하는 것이 아니라 행렬로 한 번에 처리하므로 max len 또한 1이 된다.
- complexity per layer
-
Recurrent
- complexity per layer
: recurrent에서는 Wh와 hidden state (dxd) x (dx1) 를 곱해준다.
d x d 번의 연산이 일어나게 되고, rnn에서는 문장의 길이만큼 반복하기 때문에 , n x d x d 번의 계산이 일어나게 된다. 그렇기 때문에 complexity per layer가 $O(nd^{2})$이 된다. - sequential operaions & maximum path length
: RNN은 GPU가 아무리 많아도 순차적으로 진행이 되기 때문에 N번을 반복하는 수 밖에 없다.
1번째 word 에서 n번째 word로 가기 위해서는 그 사이 word n개를 거치는 방법밖에 없기 때문에 max len이 n이 된다.
- complexity per layer
📌 transformer의 성능

기존 seq2seq보다 좋은 성능을 보이고 있다.
근데 생각보다 큰 차이는 없어서 실망했다. 참고로 BLEU 점수는 100점 만점과 같은 게 아니고 아래와 같은 지표를 가진다.

'Naver Ai Boostcamp' 카테고리의 다른 글
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |
|---|---|
| [DAY 20] self-supervised pretrained model - Bert , GPT (0) | 2021.02.20 |
| [DAY 18] Seq2seq , beam search , BLEU (1) | 2021.02.17 |
| [DAY 17] RNN & LSTM & GRU (0) | 2021.02.17 |
| [DAY 16] Bag-of-Words & Word2Vec, GloVe (0) | 2021.02.15 |