DAY23 ~ DAY24에 학습한 추천시스템을 기초부터 심화까지 학습정리한 내용입니다.
- 신기정 교수님 강의 자료
- Mining Massive Datasets : www.youtube.com/channel/UC_Oao2FYkLAUlUVkBfze4jg/videos
- MMDS PDF : www.mmds.org/mmds/v2.1/ch09-recsys1.pdf , www.mmds.org/mmds/v2.1/ch09-recsys2.pdf
📌 우리 주변의 추천 시스템
아마존의 상품추천, 넷플릭스의 영화추천, 유튜브의 영상 추천,페이스북의 친구 추천 등 많은 기업이 사용자 각각이 구매 혹은 선호할만한 상품을 추천해준다.
추천 시스템의 핵심은 사용자별 구매를 예측 혹은 선호를 추정하는 것이다.
이것을 그래프 관점에서 보면 이종그래프에서 사용자는 정점, 구매 혹은 선호는 간선으로 바라볼 수 있다.
사용자별 구매 예측은 미래의 간선을 예측하는 것으로, 선호도를 추정하는 것은 누락된 간선의 가중치를 추정하는 것으로 바라볼 수 있다.

📌 내용 기반 추천 시스템 (content-based recommender systems)
각 사용자가 구매/만족했던 "상품"과 유사한 것을 추천해주는 방법이다.
예를 들어 스파이더맨 영화를 본 사람에게 마블 영화들을 추천해주는 거다.
1. 사용자가 선호했던 상품 프로필을 수집한다.
원-핫 인코딩이 상품 프로필이 된다면 각각의 차원은 상품의 특성을 의미한다.

2. 사용자 프로필(user profile)을 구성한다.
예를 들어 사용자가 봤던 영화가 100개라면 그 100개에 대해 선호도를 이용하여 가중평균 해 계산 합니다.

3. 다른 사용자들의 상품프로필과 매칭을 통해 유사도를 계산한다.
이때 유사도는 코사인 유사도를 사용한다.
코사인 유사도는 높을 수록 해당 사용자와 다른 사용자의 취향이 유사한 것이라고 판단한다.
4. 계산한 코사인 유사도가 높은 상품들을 추천한다.
결국 내용기반 추천시스템은 어? A샀어? 그러면 다른 애 중에 A랑 B 같이 산 애 있는데 B 추천해줄게~! 다.
-
내용 기반 추천 시스템의 장단점
| 장점 | 단점 |
| - 다른 사용자의 구매기록 필요x (자신의 취향만 고려) - 독특한 취향자의 사용자에게도 추천 가능 - 새 상품에 대해서도 추천 가능 - 추천의 이유가 명확 |
- 상품에 대한 부가 정보(상품 프로필) 이 없는 경우 사용X - 구매 기록이 없는 사용자에게는 사용X - 과적합으로 협소한 추천의 위험이 있음 |
📌 Collaborative Filtering (협업 필터링)
유저 기반 (user_baed)와 아이템 기반(item_based) 필터링이 존재한다.
- 유저기반
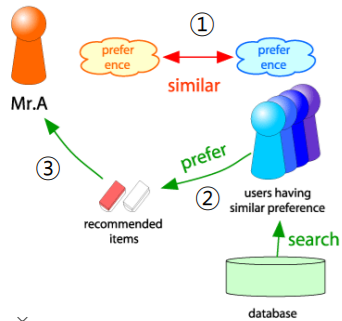
1. 추천 대상자 x 와 유사한 취향의 사용자들을 찾는다.
2. 유사한 취향의 사용자들의 선호 상품을 찾는다.
3. 이 상품을 x에게 추천해준다.
핵심은 "유사한 취향의 사용자"를 찾는 것이다.
협업 필터링에서는 유사도를 구할 때 코사인 유사도가 아닌 "피어슨 상관계수"를 사용한다.
상관계수는 -1 ~ 1 사이로 나오고 -1에 가까울수록 취향 정반대, 1 에 가까울수록 유사하다.

❓❗ 취향이 무난해서 모두 다 평점이 같은 사람은 어떡할까?
: 결론부터 말씀드리자면 해당 방법을 사용하였을 때에는(Pearson Coefficient를 유사도 함수로 사용한 Collaborative Filtering) 모든 영화의 평점을 똑같이 준 유저에 대한 추천이 불가능합니다.
하지만, 예를 들어 다른 유사도 함수(코사인 유사도)를 사용할 시에는 평균 평점을 빼주지 않고도 계산이 가능하기 때문에(성능 향상을 목적으로 유저별 평균 평점을 빼주기도 합니다. 유저별로 평점을 주는 기준이 다르기 때문에) 해당 유저에 대한 추천이 가능해집니다.

취향 유사도를 계산해보면 지수와 제니는 0.88로 취향이 유사하고, 지수와 로제는 -0.94로 상이하다.
취향의 유사도를 가중치로 사용해 평점의 가중평균으로 이 사람이 만약 이 영화를 봤을 때의 평점을 추정한다.
사용자 x가 상품 s에 대해 내릴 평점을 추정한다고 가정해보자 .
우선 상품s를 구매한 사람들과 사용자 x의 취향 유사도를 계산한다.
이후 취향 유사도가 높은(가장 취향이 유사한) 사람들 k명의 평점정보들을 가져온다.
x와 기존 사용자와의 취향유사도에 기존 사용자의 평점을 곱한 가중평균을 계산한다.
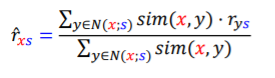
이런식으로 x가 아직 구매하지 않은 모든 상품들에 계산한 후, 추정한 평점이 가장 높은 상품을 추천해준다.
- 아이템 기반
유저기반과 유사하지만 "아이템"에 대한 유사도를 계산한다.
상관계수가 아닌 코사인 유사도를 통해 아이템들끼리의 유사도를 계산한다.
추천 대상자 x에 대해각 아이템 별 x의 선호도를 가져온 뒤, 아이템 별 유사도가 높은 순으로 아이템을 가져와 평점과 함께 가중평균을 계산한다. 이런 식으로 모든 상품에 대해 계산 후, 추정한 평점이 가장 높은 상품을 추천해준다.
- 협업 필터링의 장단점
| 장점 | 단점 |
| 상품에 대한 부가정보가 없는 경우 사용 가능 사용자의 취향이 반영된 개인화된 정보 |
충분한 수의 평점 데이터가 누적되어야함 (cold start) 새 상품, 새로운 사용자에 대한 추천 X 독특한 취향의 사용자 추천 X |
📌 평가 지표

훈련데이터를 이용해 추정한 점수를 평가데이터와 비교해 정확도를 측정한다.
평균 제곱 오차 (MSE) 혹은 평균 제곱근 오차 (RMSE)가 사용된다.
Further question
추천시스템의 성능을 측정하는 metric이 RMSE라는 것은 예상 평점이 높은 상품과 낮은 상품에 동일한 페널티를 부여한다는 것을 뜻합니다. 하지만 실제로 추천시스템에서는 내가 좋아할 것 같은 상품을 추천해주는것, 즉 예상 평점이 높은 상품을 잘 맞추는것이 중요합니다. 이를 고려하여 성능을 측정하기 위해서는 어떻게 해야 할까요?
: Recall@k, Precisoin@k, MAP, MRR, NDCG 등의 랭킹 기반 메트릭을 활용한다.
참고해서 공부할 블로그 : yamalab.tistory.com/119
📌 기본 잠재 인수 모형 ( latent factor model )
- SVD와 Matrix factorization
latent factor model의 핵심은 matrix factorization인 거 같다. (아님 말구,,,)
SVD는 이 블로그에서 설명을 기똥차게 잘해놨다.
SVD 차원 감소에 대해 먼저 얘기해보면 data들을 n차원 위의 점들로 표시를 할 수 있을 때, 아래 그림들과 같이 모든 점들은 아니지만, 대부분의 점들을 n보다 작은 차원으로 설명을 할 수 있다.
즉 n차원에 존재하는 data들을 k(<n)차원의 공간상에서 충분히 설명을 할 수 있는 것이다.
예를 들어 [1,0,0] , [0,1,0] , [0,0,1]을 basis로 span하는 3차원 공간이었다면 이는 [1,2,3] , [2,5,3]등으로 span되는 2차원 공간으로 data들을 설명하는 것이다.

SVD 분해를 했을 때, 3번째 차원의 singular vector, value가 비교적 작으니, 3차원의 data들을 2차원으로 설명할 수 있게 된다. 원래 있던 행렬 A와 값이 정확히 같지는 않지만 근사하게 된다. 잠재 인수모형에서는 이렇게 벡터를 제일 잘 설명해줄 수 있는 factor를 학습하는 것이다.

이런 식으로 차원을 감소시켜 정말 의미있는 , 이 행렬을 표현하는데 큰 기여를 하는 factor들만 추릴 수 있게 된다.

- Latent Factor Model
잠재 인수모형은 사용자와 상품을 벡터로 표현(임베딩)한다.
그러면 N차원 위에 점들로 사용자와 상품 모두를 표현할 수 있게 된다.
이 데이터들을 표현하기 위해 필요한 효과적인 인수를 학습하는 것을 목표로 하며, 학습한 인수를 잠재 인수라고 한다.
아래 사진과 같이 latent factor가 의미하는 것이 만약 성별,재미였다면 2차원 공간 내에 영화와 사용자를 한 점으로 표현할 수 있게 된다. 가까울수록 유사도가 높다고 생각할 수 있기 떄문에, 유저에게 가까운 영화를 추천해줄 수 있게 된다.

사용자와 상품을 임베딩하는 기준은 사용자와 상품의 임베딩의 내적이 평점과 최대한 유사하도록 하는 것이다.
사용자 x의 임베딩을 $p_{x}$ , 상품 i의 임베딩을 $q_{i}$ , 사용자 x의 상품 i에 대한 평점을 $r_{xi}$라고 하자.
임베딩의 목표는 $p_{x}^{T}q_{i}$가 $r_{xi}$와 유사해지도록 하는 것이다.

사용자 수의 열과 상품수의 행을 가진 평점 행렬을 R , 사용자들의 임베딩을 P , 영화들의 임베딩을 Q라고 해보자.
Q의 한 행은 item하나를 의미하고, P의 행 ($P^{T}$ 의 열)은 유저 한 명을 의미한다.
여기서의 P , Q 는 SVD로 따지면 Q = U , $P^{T}$는 $\Sigma V^{T}$로 표현된다.
R과 $QP^{T}$와 같지는 않지만 최대한 근사하도록 학습을 진행한다.
그렇기에 목적함수가 둘의 차를 최소화하는 것(SSE)으로 구성이 된다.
SVD와 다르게 latent factor model에서는 결측치에 대해서는 고려하지 않는다.
훈련 데이터에 있는 평점에 대해서만 계산한다.

하지만 위 손실함수를 사용하면 훈련 데이터의 noise까지 학습해 과적합이 발생해 오히려 성능이 감소할 수도 있다.
overfitting을 방지하기 위해 generalize를 좀 해줘야한다.
그래서 weight decay처럼 정규화항을 손실함수에 더해줘 조절해준다.
오차를 줄이는 것에도 집중하면서, 모형 복잡도를 줄일수도 있게 된다.

이렇게 극단적인, 절댓값이 너무 큰 임베딩을 방지하는 효과가 있다.
저 카우보이의 임베딩의 절댓값이 너무 커 저기 떨어져있을 때, 정규항이 없다면 이것도 패턴으로 학습해버린다.
하지만 정규항을 넣어줘서 절댓값을 작게 만들어서 generalize해줄 수 있다.

목적함수와 세트로 나오는 최적화기법! SGD를 사용해서 불안정하지만 더 빠르게 감소시킨다.
📌 고급 잠재 인수 모형 ( extending latent factor model to include biases)
- 사용자와 상품의 편향을 고려한 잠재 인수 모형
기존의 latent factor model에 전체 평균 , 사용자 편향 , 상품편향을 고려하게 된다.
사용자 편향은 사용자의 평점 평균과 전체 평점 평균의 차를 얘기한다.
한 유저가 비평가라서 다른 사람들보다 평점을 훨씬 낮게 줄 수도 있다. 이러한 경우를 고려해서 사용자 편향도 계산하게 된다. 예를 들어 전체 평점 평균은 3.7 , A가 본 모든 영화에 매긴 평점의 평균이 3.0이라면 A의 사용자 편향은 -0.7이 된다.
상품의 편향은 해당 상품에 대한 평점 평균과 전체 평점 평균의 차를 얘기한다.
만약 영화 기생충의 평점 평균이 4.5라면 기생충의 편향은 0.8이 된다.


개선된 잠재 인수모형에서 편향에 대해서도 normalize term을 준다.
편향인 $b_{x} , b_{i}$ 도 q,p처럼 파라미터로 학습한다.
SGD를 통해서 손실함수를 최소화 하는 잠재인수와 편향을 찾아낸다.

- 시간적 편향을 고려한 잠재 인수 모형
2004년 초반에 netflix의 GUI가 좋아지면서 평균 평점이 크게 상승하는 사건이 있었다.

영화의 평점은 출시일 이후 시간이 지남에 따라 상승하는 경향을 갖는다.
처음에는 이 영화를 나오기를 기다리던 사람들만 보다가, 점점 시간이 흐르면서 다른 유저들에게도 추천이 되면서 영화 출시 이후 시간이 흐르면서 평점이 변화된다.

이런 시간적 편향을 고려해 , 사용자 편향($b_{x}$)과 상품편향($b_{i}$)을 시간에 따른 linear한 함수로 가정을 한다.

'Naver Ai Boostcamp' 카테고리의 다른 글
| [Day 25] GNN 기초 & GNN 심화 (0) | 2021.03.02 |
|---|---|
| [Day 24] 정점 표현 (0) | 2021.02.27 |
| [Day 23] 군집 탐색 (0) | 2021.02.24 |
| [Day 22] 페이지랭크 & 전파 모델 (0) | 2021.02.23 |
| [Day 21] 그래프 이론 기초 & 그래프 패턴 (0) | 2021.02.22 |