📌 정점 표현 학습
DAY24에서 봤던 변환식 정점 표현 학습의 문제점은 다음과 같았다.
- 학습이 진행된 이후 추가된 정점에 대해서는 임베딩을 얻을 수 없다.
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해두어야 한다.
- 정점이 속성 정보를 가진 경우에 이를 활용할 수 없다.
변환식 정점 표현 학습이 만약 곰에게 생선을 주는 거라면 , 귀납식 정점 표현 학습은 곰에게 생선 잡는 방법을 알려주는 거다.
귀납식 임베딩 방법은 입력으로 정점들을 넣어주었을 때, 출력으로 함수 역할을 하는 인코더를 얻는 방식이다.
그래프 구조와 정점의 부가정보를 활용하는 복잡한 함수인 Encoder를 만들어 변환식 정점 표현이 가지는 문제점을 해결하게 된다.
📌 그래프 신경망 구조 (Graph Neural Network)
그래프 신경망은 그래프와 정점의 속성정보를 입력으로 받는다.
input : 그래프 , 정점의 속성 정보
그래프의 인접행렬 (adjency matrix)를 A라고 하면 A는 |V| x |V| 크기로, 각각의 노드끼리 연결되었는지를 0과 1로 표현하고 있다.
각 정점 u의 속성벡터를 $x_{u}$라고 하면 정점 속성벡터는 m차원 벡터이며, 이 m차원은 속성의 수를 의미한다.
이런 속성은 온라인 소셜 네트워크에서의 사용자 지역, 성별, 연령 ,프로필 사진
논문 인용 그래프에서의 사용자 키워드에 대한 원 핫 벡터 등 여러가지가 있을 수 있다.
아래 사진에서는 정점이 6개고 속성이 지역,성별,연령,프로필 4개이므로 정점 속성 벡터는 4차원이고, 이런 벡터가 6개 쌓여 6x4 크기의 행렬 X를 만들 수 있다.

이웃 정점들의 정보를 집계하는 과정을 반복해 임베딩을 얻게 된다.
대상 점점의 임베딩을 얻기위해 이웃들 , 그리고 이웃들의 이웃들의 정보를 집계한다.
각 집계 단계를 층(Layer)이라고 부르고, 각 층마다 임베딩을 얻는다.
layer를 늘린다는 건의 graph의 hop을 증가시키겠다는 것과 같은 의미다.
각 층에서는 이웃들의 이전 층 임베딩을 집계하여 새로운 임베딩을 얻는다.
정점 A에 대해서 임베딩을 얻기 위해, 정점 A의 이웃인 B,C,D의 이웃의 임베딩을 얻고,
B,C,D의 이웃의 임베딩을 얻기 위해서 각각의 이웃을 얻어야한다.
이 때 layer0에 해당하는 노드들(입력층)에 대해서는 정점의 속성 벡터($x_{u}$)를 사용한다.

대상 정점마다 집계되는 정보가 상이하다.
대상 정점 별 집계되는 구조를 계산그래프라고 부른다.

위 두 그림 다 잘보면 레이어별로 집계함수 색깔이 동일하다.
서로 다른 타겟 정점간에도 layer별 집계함수를 공유한다. layer끼리는 공유하지 않는다.
그러면 타겟정점마다 인풋의 개수가 달라진다. 가변적이다.
a를 임베딩할 땐 layer1에 대해서도 2개 ,4개, 1개 등 집계함수에 들어오는 input의 개수가다르다.
서로 다른 구조의 계산 그래프를 처리하기 위해서 어떤 형태의 집계함수가 필요할까?
두가지 단계로 이루어진다.
1 ) 이웃들의 정보의 평균을 계산한다. (average messages from neighbors)
2 ) 신경망에 적용한다. (apply neural network)
이웃들의 정보를 평균내서 계산하게 되면 인풋으로 들어오는 개수와 상관없이 하나만을 내보내게 된다.
두가지 과정을 거치는 집계함수를 하나의 수식으로 표현하면 아래와 같아진다.

식이 RNN과 비슷하지 않나? ㅎㅎ,,,

GNN에서는 이웃들의 정보를 합쳐 평균을 내고, 그 후 자신의 이전정보와 합쳐 임베딩 값을 구한다.
$W_{k} , B_{k}$를 학습하고, 이게 바로 layer별 신경망의 가중치(서로 다른 타겟정점간 공유)가 된다.
마지막 층에서의 정점 별 임베딩이 해당 정점의 출력 임베딩이 된다.
복잡해보이는데 이 과정을 그림으로 되게 잘 표현한 블로그가 있어서 가져와봤다.

비지도 학습 방식으로 loss fuction을 결정할 수 있다.
loss fuction의 목적은 정점 간 거리를 보존하는 것이다.
이전에 나왔던 random walks, graph factorization 등의 loss fuction을 가져다 쓰면 된다고 한다.
그냥 제일 가장 심플하게 그래프에서의 인접성을 기반으로 유사도를 정의하면 아래와 같이 쓸 수 있다.
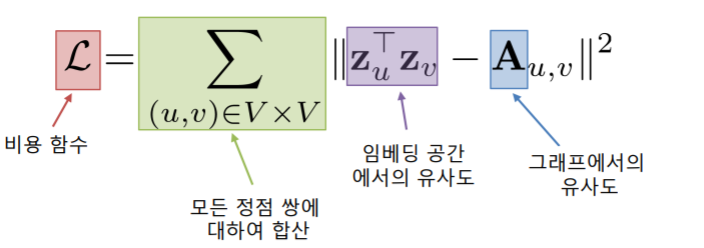
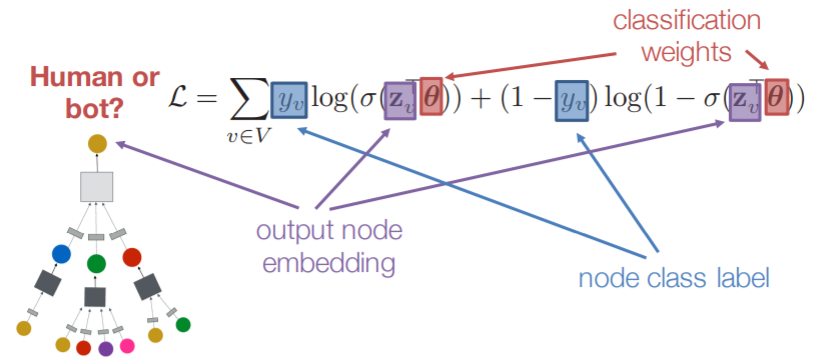
downstream과 함께 지도학습 방식으로도 loss fuction을 이용한 end-to-end 학습도 가능하다.
예를 들어 task가 정점 분류인 경우 정점의 임베딩을 얻고, 분류기의 입력으로 넣어, 각 정점의 유형을 분류해야한다.
이때 loss fuction은 task에 맞게 cross entropy를 쓰고, backpropagation을 통해 embedding도 학습할 수 있게 된다.
📌 그래프 합성곱 신경망(Graph Convolutional Network : GCN)
부터는 논문 읽고 더 공부해서 쓰는 걸로 ㅠㅠ
근데 그래프 인간적으로 너무 재밌는 거 아닌가?
'Naver Ai Boostcamp' 카테고리의 다른 글
| [DAY 31] Image classfication1 & annotation data efficient learning (0) | 2021.03.13 |
|---|---|
| [Day 26] 특강 및 자율 공부 (0) | 2021.03.03 |
| [Day 24] 정점 표현 (0) | 2021.02.27 |
| [Day 23.5] 추천시스템 (기초 ~ 심화) (0) | 2021.02.26 |
| [Day 23] 군집 탐색 (0) | 2021.02.24 |