"나는 수학을 싫어해" 라는 텍스트에 대해서 사람은 이해할 수 있지만 , 컴퓨터는 바보라서 이해할 수 없다.
컴퓨터가 이해할 수 있도록 텍스트를 숫자로 이루어진 벡터로 변형(수치화)시켜 주어야 한다.
단어를 벡터로 표현하는 방법에는 여러가지 방법이 있다.
Bag of words
bag of words는 단어들의 순서를 고려하지않고 "빈도수"에 집중해 텍스트를 표현하는 방법이다.
말 그대로 모든 단어들을 가방에 다 집어넣게 되므로 순서 같은 건 고려하지 않게 되며, 갯수에만 의존하게 되는 것이다.

엄청 엄청 엄청 간단하다.
한 문서에 다음과 같은 두 문장이 있다고 하자.
"John really really loves the movie"
"jane really likes this song"
1. 두 문장에 대해 중복을 고려하지않고, unique한 단어들이 담긴 사전을 하나 만들 수 있다.
{"john" , "really" , "loves", "this" ,"movie" , "Jane", 'song"}
2. 유니크한 단어들을 one-hot vector들로 인코딩해준다.
총 8개의 단어들로 사전이 이루어져있으니, 8차원의 one-hot vector로 만들어준다.

이렇게 되면 모든 단어들 끼리는 서로 유클리드 거리가 $\sqrt{2}$로 똑같아지며, 코사인 유사도 = 0 을 가지게 된다.
즉 bow를 사용하게 되면 단어들은 서로의 맥락, 의미들과 관계없이 모두 동일한 관계가 되는 것이다.
두 과정을 거치게 되면 한 문장/문서를 one-hot-vector들의 합으로 표현할 수 있게 된다.
"John really really loves the movie" 의 경우 john 1번 , really 2번 loves 1번 the 1번 movie 1번으로 원핫벡터들을 모두 더하면 [1,2,1,1,1,0,0,0]으로 표현할 수 있다.
📌 bow의 한계점
요렇게만 봐도 bow의 문제점이 드러난다. 내가 생각하는 문제점을 몇 개 써보자면,,,
1. "The movie really really loves Jones" 와 같이 문장을 써도 윗 문장과 같은 원핫벡터들의 합으로 표현이 되버린다. (물론 이런 문장은 쓰일 일이 없겠지만 ㅎㅎ,,,) 말이라는 게 "아" 다르고 "어" 다른 것인데 순서를 전혀 고려하지 않기때문에 발생하는 일이다. John이 movie를 좋아하는 것인지, movie가 John을 좋아하는 것인지 의미가 모호해져버린다.
2. "빈도 수"에만 집중하게 된다. "a" , "the"와 같은 어쩔 수 없이 모든 문장에 많이 쓰이는 단어들이 있는데, 어떤 두 문장이 문맥적으로는 굉장히 유사하지만 겹치는 단어가 많이 없다면 두 단어 사이의 유사도가 떨어진다고 판단해버리게 된다.
이를 조금이나마 해결하기 위해서 a, the와 같은 걸 "불용어"라고 하며, 사용자가 사전에 불용어 사전을 미리 만들어놓고 그에 해당하는 단어는 빼버릴 수도 있다.
3. "희소표현"이기 때문이다.
단어들을 one-hot vector로 표현하기 때문에 공간낭비가 엄청 심하다.
만약 중복없이 단어들이 1억개가 있다면 하나의 단어는 1억 차원의 크기를 가지게 된다.
bow를 사용해 텍스트를 벡터화시켜 bert 같은 모델에 쓴다고 생각하면 🤦♀️ 차원의 저주에 걸리게 된다.
희소표현은 0이 많아야 하는 거 아닌가?
"John really really loves the movie" = [1,2,1,1,1,0,0,0] 으로 0이 많지 않은데? 라고 생각할 수도 있지만, 어쨌든 저 단어들 하나하나를 다 0과 1로 이루어진 one-hot 으로 표현해야기때문에 희소표현과 동일하다.
❓❗희소벡터 vs 밀집벡터
선형대수에도 나오는 표현이다.
벡터 or 행렬의 대부분이 0으로 이루어져있다면 0을 제외한 수들이 얼마없이 희소하니까 희소표현 ㅎ,,,,
그래서 one-hot vector가 대표적인 희소벡터다.
예를 들어 소설 책 한 권을 데이터로 사용한다고 하면 , 거기 사용된 단어들은 최소 몇 만개는 될 것이다.
그러면 I라는 단어 하나를 표현하기 위해서 하나만 1이고 나머지는 모두 0인 몇 만 차원의 벡터를 사용해야된다.
밀집벡터는 반대로 실수값들이 오밀조밀 모여있는 벡터들을 얘기한다.
유니크한 단어의 수 = 벡터의 차원이었던 원핫과는 다르게 밀집벡터는 사용자가 차원을 정해준다.
예를 들어 차원을 5로 고정했다면, I라는 단어는 [0.2 , 2.1 , -0.1 , 5.3 , -3.1]과 같이 표현할 수 있게 된다.
📌Naive Bayes Classifier
Bow를 사용해서 뭘 할 수 있을까? 메일이 왔을 때 이를 스팸인지 아닌지 구분하는 것과 같은 classification문제에 사용해볼 수 있다. 나이브 베이즈 분류기는 딥러닝을 사용한 알고리즘은 아니지만 간단하면서도 효과가 있다.
www.cs.columbia.edu/~mcollins/em.pdf를 참고하였다.
나이브 베이즈 분류기의 목표는 여러 단어들( $x_{1} , x_{2} , x_{n}$)로 이루어진 어떤 문장이 주어졌을 때, 카테고리 별 확률을 구해 이 문장을 분류 하는 것이다.
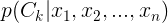
위 식을 posterior로 바라보면 Bayes'rule을 사용하여 각 카테고리별 확률을 구할 수 있게 된다.

모든 카테고리에 대해서 $x_{1} , x_{2} , \cdots, x_{n}$ 이 나올 확률은 동일하므로 분모는 무시하고 분자에 집중해보자.
각 x들이 서로 독립적이며 동일한 확률분포를 가진다고 하면 n개의 $x_{i}$들에 대해서 조건부 확률들의 곱으로 표현할 수 있게 된다.

MLE(Maximum Likelihood Estimate)를 통해서 파라미터인 $p(C_{k})$, $p(x_{i} | C_{k})$를 구할 수 있다.
카테고리분포를 따르고 있으므로, 각 class가 나올 확률 = class가 나온 횟수 / 전체 시행 횟수가 된다. \begin{align}p(C_{k}) = \frac{\sum_{n}^{}c = c_{k}}{n} = \frac{count(c_{k})}{n}\end{align} \begin{align}p(x_{i}|C_{k}) = \frac{\sum_{n}^{}c = c_{k} \, and \, x = x_{i}}{\sum_{n}^{}c = c_{k}} = \frac{count(x_{i}|c_{k})}{count(c_{k})}\end{align}
수식으로 쓰면 어려워보일 수 있는데, 예제로 보면 엄청 쉽다.
아래와 같이 training 데이터가 주어졌다면
$p(C_{cv}) : $CV가 나올 확률 = $p(C_{nlp}) : $NLP가 나올 확률 = 0.5가 된다.

각 단어 $x_{i}$에 대해 해당 클래스가 나올 때 해당 단어가 나올 확률인 $p(x_{i} | C_{k}$를 계산해 각각 곱해주면


위와 같이 각 test시 주어진 문장이 각각의 class 에 해당하는 확률을 계산할 수 있게 된다.
CV일 때의 확률이 더 높으니 이 문장은 CV로 분류된다.
➕ 연속확률분포를 따르는 데이터들에 대해 나이브베이즈 분류하는 법을 써놓은 포스팅이다.
똑같이 MLE를 통해 학습하지만 연속확률분포기때문에 카테고리가 아닌 가우시안 분포를 따른다는 게 다르다.
arkainoh.blogspot.com/2018/08/parametric.classification.nbc.continuous.probability.distribution.html
📌Naive Bayes Classifier의 한계점
- Bow와 똑같이 순서관계를 고려하지 않고, 중복되는 단어의 빈도수에만 집중한다.
- 하나라도 0이 나오게 되면 값 자체가 0이 되어버린다.
예를 들어 새로운 문장에 "usually"와 같이 이전 문장에는 없던 단어가 들어가있다고 생각해보면 class likelihood가 0이 되어 다른 값들에 상관없이 0이 곱해지기때문에 확률이 0이 되어버려 다른 값들을 무의미하게 만들어버린다.
이를 해결하기 위한 방법으로 일종의 가중치,편향을 조금씩 더해준다.=> Laplace smoothing
📌 Word Embedding : Word2Vec , GloVe
word embedding이란 하나의 단어를 벡터로 표현하는 방법 중 하나이다.
어떤 단어를 R차원의 벡터로 mapping 시켜주는 것을 뜻한다.
"cat"이란 단어를 아래 그림처럼 실수들로 이뤄진 r차원의 벡터들로 mapping 시켜주는 W가 바로 word embedding이다.

Bow가 단어 집합의 크기만큼을 차원으로 가지는 0과 1로 이루어진 벡터였다면 , 임베딩 벡터들은 사용자가 하이파라미터로 준 차원만큼의 크기를 가진다. 또 가중치를 학습하는 것과 같은 방식으로 단어 벡터를 학습하게 된다.
word embedding을 사용하면 단어들간의 유사도, 관계를 알 수 있다.
이전 Bow와 같이 one-hot으로 나타내게 되면 모든 단어간의 거리, 유사도가 같기 때문에 단어들간의 관계를 알 수 없었다.
하지만 word embedding을 사용하게 되면 하나의 단어를 R차원 위의 한 점으로 표현할 수 있게 된다.
기본적으로 "비슷한 의미를 가진다면 비슷한 위치에서 등장한다" 라고 가정하기 때문에 서로 관계가 있는 단어들은 비슷한 위치에 등장하게 돼 거리가 짧아진다.
예를 들어 cat, kitty같은 경우 둘은 비슷한 의미를 가지고 있으므로, embedding vector 사이의 거리가 짧아 근처에 위치해있고 hamberger와 같이 뜬금없는 단어와는 vector끼리의 거리가 멀다.
여기서 말하는 "유사"는 꼭 비슷한 것들만이 아니라, 서로 연관이 있는 단어들을 얘기하는 거 같다.

📌 Word2Vec
word2vec에는 주변 단어를 가지고, 중간에 있는 단어를 예측하는 CBOW와 주변 단어를 가지고, 중간 단어를 예측하는 Skip-gram 두 가지 방식이 있다.
word2vec의 기본 아이디어는 같은 문장 내에서 단어들이 인접하다면 서로 의미가 비슷하다고 가정한다.
이 후 주변단어 (context word)를 이용하여 중심단어(center word)를 예측한다.
그냥 convolution에서 kernel의 weight를 학습하는 것과 똑같다.
문장에 대해서 for문을 한 번 돌리듯 첫 단어부터 끝단어까지 하나하나 중심단어로 정한다.
중심단어에 대해서 양옆으로 몇 개의 단어를 고려하는데 이를 sliding window라고 한다.
window가 2라면 양옆으로 2개씩 총 4개를 고려하는 것이다.
중심단어를 예측할 때, window에 해당하는 단어들이 고려된다.
아래 그림에서는 I를 예측하니 왼쪽은 없으니 PASS! 오른쪽 study , math를 고려해준다.
one-hot vector를 input으로 받아 사용자가 정해준 hidden layer의 차원으로 변환된다.
이때 input layer에서 hidden layer로 가게 해주는 weight가 곧 임베딩 벡터가 되니 엄청나게 중요하다.
VxM (사전의 크기 x 임베딩 벡터의 크기 ) 로 각각의 행이 곧 임베딩 벡터가 된다.
이후 다시 MxV크기의 W2와 곱해져 output을 내보낸다.
W2의 열벡터도 임베딩벡터가 될 수 있다.
W1의 행벡터 , W2의 열벡터 둘 중 하나를 임베딩 벡터로 사용해도 되고, 둘을 평균내 사용해도 된다.
이후 softmax 함수를 거치고 cross entropy를 계산해 오차를 줄이는 쪽으로 W들이 학습된다.

ground truth 에 해당하는 label은 무한대에, 나머지는 -무한대에 가까워져야 loss가 최소화된다.
input이 one-hot vector기 때문에 window에 해당하는(노란색으로 색칠한 부분)만 weight가 계산이 된다.
결국 study , math는 I와 큰 유사도를 가지게 된다.

word vector들끼리 빼보면 두 단어 사이의 관계를 알 수 있는데, 같은 관계를 가지는 임베딩 벡터들은 방향이 똑같다.

ronxin.github.io/wevi/ Word embedding을 시각화 한 사이트다. 여기 들어가보면 신세계를 경험할 수 있다!!
Intrusion Detection 이라는 주어진 단어에서 가장 의미가 상이한 단어를 고르는 그런 task도 할 수 있다.
임베딩 벡터들의 유클리드 거리 평균을 구해 가장 평균이 크다면 가장 상이한 단어가 되는 것이다.
word2vec은 이외에도 기계번역 , 감정분석 , 클러스터링,이미지 캡셔닝 등 여기저기서 많이 사용된다.
📌 GloVe
word2vec은 window내만 고려하기 때문에 문장의 전체적인 정보를 이해할 수 없다.
이러한 word2vec의 단점을 개선하기 위해 GloVe가 탄생했다. 물론 word2vec만의 단점은 아니다!!
Glove는 두 단어가 하나의 window 내 몇 번 동시 등장했는지를 사전에 미리 계산한다.
이를 카운트한 표가 co-occurrence matrix다.
I like deep learning
I like NLP
I enjoy flying
i단어의 윈도우 내 k단어가 등장한 횟수를 i행 k열에 써넣는다.
윈도위의 크기가 1이라 바로 좌우만 고려한다고 가정하면 co-occurrence matrix는 아래처럼 된다.

co- occurrenc matrix를 기반으로 동시등장확률(co-occurence probablity)를 계산할 수 있다. $P(k\ |\ i)$ 는 특정 단어 i의 전체 등장 횟수를 카운트하고, 특정 단어 i가 등장했을 때, 어떤 단어 k가 등장한 횟수를 카운트하여 계산한 조건부 확률이다.

특정 단어 k가 주어졌을 때 임베딩 된 두 단어 벡터의 내적이 두 단어의 동시등장확률 간 비율이 되게 임베딩함
즉 solid라는 단어가 주어졌을 때, ice와 stream의 내적값이 8.9가 되도록 임베딩하려고함
i번째 단어와 j번째 단어의 내적과 한 윈도우 내 두 단어가 등장한 확률의 차이를 최소화하는 목적함수를 만들었다.
\begin{align*}
J&=\sum _{ i,j=1 }^{ V }{ { f\left( { X }_{ ij } \right) ({ w }_{ i }^{ T }\tilde { { w }_{ j } } +{ b }_{ i }+\tilde { { b }_{ j } } -\log { X_{ ij } } ) }^{ 2 } } \\ &where\quad f(x)=\begin{cases} { (\frac { x }{ { x }_{ max } } ) }^{ \alpha } \\ 1\quad otherwise \end{cases}if\quad x<{ x }_{ max }
\end{align*}

f(x)를 추가해준 이유는 $X_{i,j}$가 특정 값 이상으로 튀는 경우를 방지하기 위한 장치

의미가 비슷한 단어들끼리는 벡터가 유사한 걸 확인할 수 있다.
Further Questions : Word2Vec과 GloVe 알고리즘이 가지고 있는 단점은 무엇일까요?
- GloVe에서 지적한 word2vec의 문제점으로는 window내만 고려하기 때문에 전체적인 문장의 맥락을 이해할 수 없다는 거다.
- bow보다 임베딩이 훨씬 파워풀하긴 하지만, word2vec자체는 input이 one-hot이라서 나는 개인적으로 비효율적이라고 생각한다,,
참고
ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/09/glove/
'Naver Ai Boostcamp' 카테고리의 다른 글
| [DAY 18] Seq2seq , beam search , BLEU (1) | 2021.02.17 |
|---|---|
| [DAY 17] RNN & LSTM & GRU (0) | 2021.02.17 |
| [DAY 15] Generative model (0) | 2021.02.05 |
| [DAY 14] Recurrent Neural Networks (0) | 2021.02.05 |
| [DAY 13] Convolutional Neural Networks (0) | 2021.02.04 |