역대급으로 어려웠던 하루,,, gan이 내가 알던 gan이 아니야,,,
1. 생성 모델 (generative model)
생성 모델이라고 하면 나도 그렇고 사람들은 단순히 이미지를 만들어내는 GAN을 생각한다.
Explicity model : 모델이 갖는 분포인 $P_{model}$의 확률 밀도 함수를 정확하게 구할 수 있는 경우
- 예시 ) X가 "개"라면 P(X)는 높을 것이고, 아니라면 낮을 것이다.(이상탐지)
- 예시가 어떻게 보면 일종의 "분류"와도 같다. 이런 점에서 엄밀한 의미의 Generative model은 discriminator도 포함한다.
Inplcity model : $P_{model}$을 정의하지 않고 샘플링을 통해 이미지 생성
: "개"를 의미하는 특정한 확률분포를 학습해 이와 유사한 분포에서 샘플링을 통해 "개"이미지를 만들어내는 과정
$P_{model}$을 어떻게 구할까?
:x란 입력을 넣었을 때, 값이 나올 수도 있고 , x를 샘플링하는 모델일 수도 있다.
❓❗ 이미지의 확률분포는 뭘까
확률분포를 검색하면 주로 주사위 예제나, 차원이 커봤자 3차원에서의 가우시안 분포 등 밖에 나오지 않는다.
이미지에서 확률분포는 무얼 뜻할까?
해당 링크에 따르면 예를 들어 100 x 100 컬러 사진이 있다면 이 사진을 100x100x3차원의 한 점으로 바라본다....
4차원부터는 상상하기도 힘든데 이를 30000차원으로 바라본다,,,,

흑백 이미지에 n개의 $X_{1} , X_{2} , \cdots , X_{n}$이라는 binary pixel이 있다.
예를 들어 28x28 MNIST 이미지라 가정하면 하나의 이미지가 가질 수 있는 경우의 수는 $2^{764}$가 된다.
확률분포 $P(x_{1} , x_{2} , \cdots , x_{n})$로부터 샘플링을 통해 이미지를 만들어야 된다.
이때, 확률분포는 chain rule에 의해 아래와 같이 표현할 수 있으며 n개의 확률변수에 대해 $2^{n}-1$개의 파라미터를 필요로 하게 된다.

만약 $X_{1} , X_{2} , \cdots , X_{n}$이 독립적이라고 가정해본다면
\begin{align}p(x_{1} , x_{2} , \cdots , x_{n}) = p(x_{1})p(x_{2})\cdots p(x_{n}) \end{align}으로 표현할 수 있다.
가능한 경우의 수는 동일하게 $2^{n}$이지만 확률분포를 명시하기 위해 필요한 파라미터의 개수는 $\textbf{n}$개 뿐이다.
서로 독립적이므로 $X_{i}$가 1이 나올 확률인 모수 하나만 구하면 되기 때문이다.
그런데 픽셀이 서로 독립적이면 될까..?
위와 같은 숫자 이미지 그니까 "어떤 모양"을 만들려면 어느정도 이만큼은 흰색~ 이만큼은 검은색~이 필요하다.
즉 실제로는 독립적일 수 없기 때지만 파라미터가 n개여서 좋긴 하지만 실제로 쓸 수 없다.
그럼 $2^{n}-1$과 $n$사이 어딘가 적절한 타협점을 찾아야 한다. 세 가지 기본 개념을 잘 버무려보면 된다.
- chain rule

- Bayes'rule
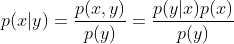
- conditional independence
\begin{align} p(x\, |\, y, z) = p(x\, |\, z)\end{align}
z가 주어졌을 때, x, y가 독립이라면 x, y는 서로에게 영향을 못 미치므로 $P(x|y,z)$는 $P(x|z)$와 같아진다.
Markov assumption : $X_{i+1}$이 직전 $X_{i}$에게만 영향을 받고, 그 이전 $X_{1} , \cdots , X_{i-1}$과는 독립이다.
확률변수 X가 Markov assuption을 따른다고 하면, 위 3가지 개념들을 잘 버무리면

위처럼 자기 이전만 영향을 받는 식으로 바꿀 수 있어서 파라미터의 개수가 2n-1개가 된다.
Autoregressive model
자신의 이전 $\tau$만큼을 참고해 미래를 예측하는 모델을 얘기한다.
Markov 가정에 의해 i시점이 i-1시점에만! 의존하는 모델도 autoregressive model이지만, 1번 시점부터 모든 히스토리에 의존적인 모델도 autoregressive 로 이런 전반적으로 자신의 이전을 참고하는 모델을 얘기한다.
잘 생각해보면 sequence데이터를 다룰 때 AR이라고 하며 얘기했었다.
"미래"를 예측하기 위해 "과거"를 고려한다 라는 말은 데이터들 사이의 "순서"가 있다는 뜻이다.
이미지에 "순서"를 정한다는 것은 명확하지 않다.
순서를 어떻게 정하느냐에 따라, 이전 시점을 얼마큼 고려하냐에 따라 모델이 달라진다.
NADE(Neural Autoregressive Density Estimator)

NADE는 explicit모델로, 단순 이미지 생성뿐만이 아니라 확률밀도함수를 구해 확률값을 계산할 수 있다.
i번째 픽셀의 확률분포를 구할 때, 1번 시점부터 i-1번 시점까지 모두 고려하여 확률밀도함수를 구한다.
1~i-1번째까지의 가중치와 곱해줘 시그모이드를 취하는 과정을 2번 반복하는 즉 hidden layer가 2개인 MLP를 사용한다.
네트워크 차원에서는 입력이 계속 달라지기 때문에, 가중치도 계속 늘어난다.
예를 들어 두번째 픽셀에 대해서는 1번 픽셀만을 고려하니 1개의 입력을 받는 weight 가 필요하지만 , 100번째 픽셀에 대해서는 1~99번 픽셀들을 고려해야하므로 99개의 입력을 받는 weight 가 필요하다.
pixel RNN
pixel RNN도 NADE와 같이 explicit 모델로, 확률값을 계산할 수 있다.
MLP 대신 RNN을 활용한 auto-regressive model이다.

R값은 i이전의 모든 픽셀들을 고려
G값은 i이전의 모든 픽셀들을 고려 + i번째 픽셀의 R 고려
B값은 i이전의 모든 픽셀들을 고려 + i번째 픽셀의 R 고려 + i번째 픽셀의 G 고려'
이런 식으로 확률밀도함수를 구하게 된다.
"순서"를 정하는 방법에 따라 Row LSTM , Diagonal BiLSTM 이렇게 두가지가 존재한다.

이 부분에 대해서는 좀 더 공부가 필요할 거 같다. 그림만 보곤 이해가 잘 안된다.
Row LSTM같은 경우, 자기 이전 행을 고려해 Hidden state(i-1,j-1)+ Hidden state(i-1,j+1)+ Hidden state(i-1,j)거 까진 알겠는데 밑 부분의 파란색 화살표는 뭘까,,,,
Diagonal BiLSTM도 자신의 pixel(i, j-1) + pixel(i-1, j)인 건 알겠지만 딱 거기까지가 끝이다,,,
연휴를 이용해 논문을 읽어본다든지 좀 더 보충할 계획이다.
Variational AutoEncoder
autoencder와 variational autoencdoer의 차이는 여기서 확인할 수 있다.
variational inference의 목표는 posterioir distribution에 아주 근사한 variational distribution을 찾는 것이다
posterioir distribution은 관측치가 주어졌을 때, 내가 관심있어하는 랜덤변수의 확률분포를 얘기한다.
근데 일반적으로 저게 불가능하다. 그래서 내가 최적화 시킬 수 있는 posterioir distribution에 근사하는 분포를 찾는 게 더 빠르다. 이게 바로 variational distribution이다.
음 좋은 예인지 모르겠지만 내가 강동원을 좋아한다고 치면,,, 강동원과 사귀는 것은 불가능에 가깝다.
그러니 차라리 일반인과 사귀어 그 친구를 강동원과 비슷하게 꾸미는 것이 훨씬 빠르다.
이 과정에서 강동원과 사귀는 것이 posterior distribution , 일반인을 강동원과 비슷해 보이게 꾸미는 것이 variational distribution이다.

posterioir distribution와의 KLdivergence를 최소화함으로써 가~~장 근사한 variational distribution을 구하는 것이 우리의 목표가 된다.
그.런.데.말.입.니.다
우리는 posterioir distribution을 모른다. 하지만 posterioir 와 가장 근사한 variational 을 구해야 한다.
생각해보면 어이가 없다. 뭔지도 모르는데 어떻게 가장 근사하지,,,? 이걸 가능하게 만드는게 "ELBO"다.

계산하기 쉬운 ELBO(Evidence Lower BOund)를 증가시킴으로써, MLE를 증가시켜 가장 근사한 variational 을 구할 수 있게 된다. ELBO를 또 2개의 term으로 나눌 수 있다.
첫번째 항은 reconstruction term으로 z가 주어졌을 때 x를 표현하기 위한 확률밀도함수 = decoder를 의미한다.
디코더의 가능도가 클수록 ,$theta\$가 decoder가 일을 잘한다 = z에서 그럴싸한 x를 잘만들어낸다.
첫번째 항은 클수록 logP가 커진다.
두번째 항은 prior fitting term으로 실제 잠재변수 z의 분포와 인코더가 x로부터 만들어낸 z 사이의 분포가 얼마나 유사한지를 나타낸다.
KL divergence가 낮을수록 둘이 유사하단 의미이므로, 두번째 항은 작을수록 모델의 가능도가 커진다.
q,p 둘 다 각 변수가 독립인 다변량 정규분포(isotropic gaussian)를 따른다고 할 경우,\begin{align*}
{ D }_{ KL }\left( q\left( z|x \right) ||p\left( z \right) \right) =&{ D }_{ KL }\left[ N\left( { \left( { \mu }_{ 1 },...,{ \mu }_{ k } \right) }^{ T }, \textrm{diag}\left( { \sigma }_{ 1 }^{ 2 },...,{ \sigma }_{ k }^{ 2 } \right) \right) ||N\left( 0,1 \right) \right] \\ =&\frac { 1 }{ 2 } \sum _{ i=1 }^{ }{ \left( { \sigma }_{ i }^{ 2 }+{ \mu }_{ i }^{ 2 }-\ln { \left( { \sigma }_{ i }^{ 2 } \right) } -1 \right) }
\end{align*}
'Naver Ai Boostcamp' 카테고리의 다른 글
| [DAY 17] RNN & LSTM & GRU (0) | 2021.02.17 |
|---|---|
| [DAY 16] Bag-of-Words & Word2Vec, GloVe (0) | 2021.02.15 |
| [DAY 14] Recurrent Neural Networks (0) | 2021.02.05 |
| [DAY 13] Convolutional Neural Networks (0) | 2021.02.04 |
| [DAY 12] 최적화 (1) | 2021.02.02 |