1. DLBasic : optimization
📌 학습목표
- Generalization,Overfitting, Cross-validation의 용어와 다양한 Gradient Descent 기법과 그에 따른 성능차이
Important concepts in Optimization
1. Generalization

처음보는 data(test data)에 대해서도 얼마나 잘 예측/분류 등을 할 수 있게 하는 것을 의미한다.
딥러닝 모델은 train data를 통해 학습해 처음보는 test data에 대해서도 좋은 성능을 낼 수 있게 하는 것이 목표다.
train error 와 test error의 차가 작을 수록 좋은데, 이 차를 generalization gap이라고 한다.
generalization performance가 좋다는 것은 generalization gap이 적은 것을 의미한다.
그럼 언제 Generalization이 잘 되고 언제 잘 안될까?
2. Under-fitting vs Over-fitting

under-fitting도 overfitting도 되지 않은 그 사이 딱 적절할 때, generalization이 잘 된다.
overfitting은 학습데이터를 과하게 학습한 경우를 얘기한다. 너무 train data에만 맞춰져버려서 train error는 굉장히 낮지만 새로 본 데이터에 대해서는 잘 성능하지못해 test error는 높아진다.
underfitting은 학습데이터조차도 잘 학습하지 못한 경우를 얘기한다.
과소적합과 과대적합 그 사이 어디쯤 적절하게 학습해야 generalization performance가 좋아진다.
3. cross validation
1 ) hold out cross validation
주어진 train set을 임의의 비율에 따라 train data + validastion data로 분할하여 사용하는 것이다.
보통 train : validation 을 7 : 3 비율로 나눠준다.
train data로 학습시킨 후, validation data 으로 검증을 해주는 것이다. 이때 test data는 사용되지 않는다.
2 ) k-fold validation

train data set을 k개로 나눈다.
k개로 나누는 기준은 랜덤, 층화,클러스터 등등 다양하다.
하나의 dataset을 validation set으로 두고 나머지 train data에 대해서 학습한 후 , validation data로 검증한다 이 과정을 k번 반복한다. 이 과정에서 test data를 사용하면 안된다.... 그럼 반칙이지,,
교수님의 설명에 의하면 최적의 하이퍼파라미터를 선정하기 위해 사용된다고 한다.
hyperparameter tunning이라고도 하는데, 하이퍼파라미터를 각자 다르게 설정한 후 cross validation을 사용하여 k개의 모델을 비교한다. 이렇게 최적의 하이퍼파라미터를 찾는다. 그 후에는 최적의 하이퍼파라미터와 train data set 전체를 이용하여 학습을 진행한다.
iteration 횟수가 너무 많아 시간이 오래걸린다는 문제점이 있지만, 데이터의 수가 적을 때 아주 효과적이다.
❗ Hyperparameter vs parameter
하이퍼파라미터 : 모델링 시 사용자가 설정해주는 값. 보통 함수를 쓸 때 인자로 설정해는 것들 ex ) 학습률, decay 등
파라미터 : 모델 내에서 결정되는 값, 사람이 결정할 수 없다. ex) weight , bias 등
4. bias and variance tradeoff

variance는 분산, 즉 추정값들이 얼마나 퍼져있는지를 의미한다.
bias는 편향, 참 값들과 추정값들의 차이를 의미한다.
(a) 는 추정값들이 적당히 잘 모여있으면서도 참값과 추정값들이 아주 유사한 가장 best한 상황이다.
(b) 는 train data에 의해 overfitting 되어 test data에 대한 추정값과 참값이 너무 많은 차이가 나는 상황이다.
(c) 는 train data를 잘 학습하지 못한 underfitting 된 상황이다.
(d) 는 b,c 둘 다 일어난 최악의 상황이다..
train data에 잘 fitting 되게 하기 위해서 모델 복잡도를 높이면 (b)처럼 overfitting 되어 loss가 증가할 수도 있다.
반대로 모델복잡도를 단순하게 만들면 학습이 덜 되어 (c)처럼 underfitting 돼 loss가 증가할 수도 있다.

loss fuction은 noise를 무시했을 때 variance와 bias의 제곱으로 이루어져있다.
LOSS를 고정해놓고 생각해보면 variance가 높아지면 bias가 낮아지고 bias가 높아지면 biasvariance가 낮아진다.
그래서 이 둘 사이의 적절한 합의점을 찾는 bias-variance trade off가 엄청나게 중요하고, generalization performance와도 직결된다.
5. bootstrap
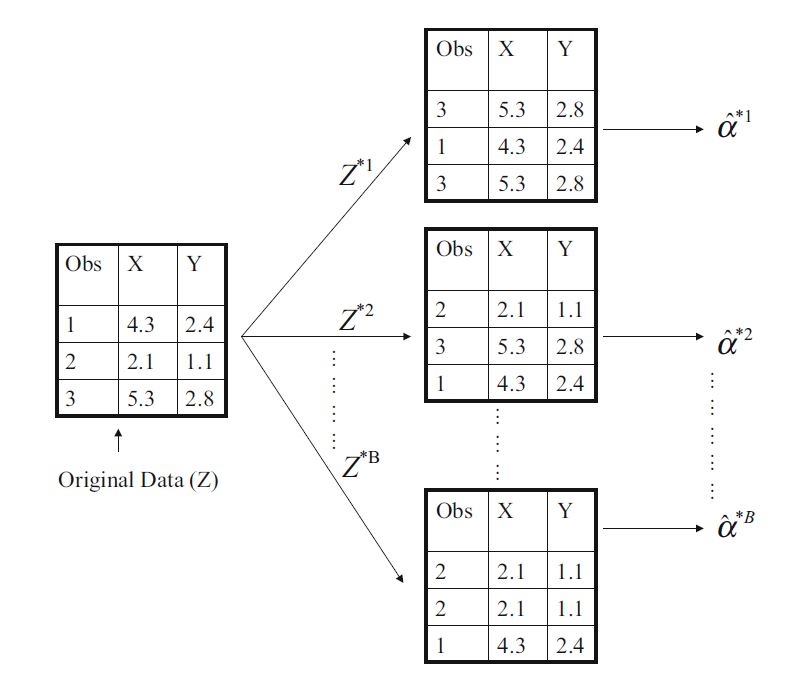
cross validation과 같이 데이터 내에서 반복적으로 resampling 하는 방법 중 하나이다.
N개의 data에 대해서 m개의 sample을 만들고싶다면, 복원추출을 m번 실행하면 된다.
실제로는 계산하기 어려운 추정량의 불확실성을 계산한다.
1) bagging (booststrap aggregation)
표본이 모집단을 잘 반영할 수 있다는 통계 개념에서 나왔다.
부트스트랩을 이용하여 N개의 데이터에서 M개의 동일한 사이즈를 가지는 sample들을 뽑아낸다.
총 M개의 각기 다른 모델들에 대해 학습을 시킨다.(하이퍼파라미터 등을 각기 다르게 줌)
이후 총 M개의 모델의 test 결과에 대해서 평균 혹은 voting방식을 사용하여 최종 output을 얻게 된다.

위 사진의 회색 선은 m개의 boost sample들로 각각 학습한 모델들의 test output이다.
여기서는 이 회색 선들의 평균을 내어 빨간색선처럼 비교적 부드러운 곡선을 얻었다.
표본데이터가 너무 작은 경우 전체 데이터를 잘 반영할 수 없으므로 이런 경우 bagging을 사용하면 안된다.
특이점이 너무 많은 경우, 데이터가 서로 의존적인 경우(Time series) 사용하면 안된다.
2 ) boosting

분류하기 어려운 특정 훈련 샘플들에 focus 된 기법이다.
무작위로 샘플링하는 것이 아닌 연속적으로 weak learner끼리 결합시켜 더 파워풀한 모델을 만들어내는 것을 말한다.
weak learner를 이용해 학습을 하면서 잘못 예측/분류한 데이터에 좀 더 집중하기 위해 가중치를 더 부여해준다.
배깅과 같이 랜덤하게 샘플링 하지만 이전 weak learner에 대해 가중치를 부여한다.
이후 모델별로 계산된 가중치를 합산하여 최종모델을 생성한다.
3 ) bagging과 boosting

| 비교 | bagging | boosting |
| 특징 | 서로 독립적인 앙상블 모델 | 이전 모델을 고려하는 sequence한 모델 |
| 목적 | variance 감소 | bias 감소 |
| 적합한 상황 | high variance , low bias | high bias , low variance |
| sampling | 무작위 복원 추출 | 무작위 복원 추출 + 가중치 부여 |
최적화 알고리즘
0.INTRO
최적화 알고리즘들에 대해 설명하기 전, 최적화 알고리즘이 왜 중요한지에 대해 생각해보자.
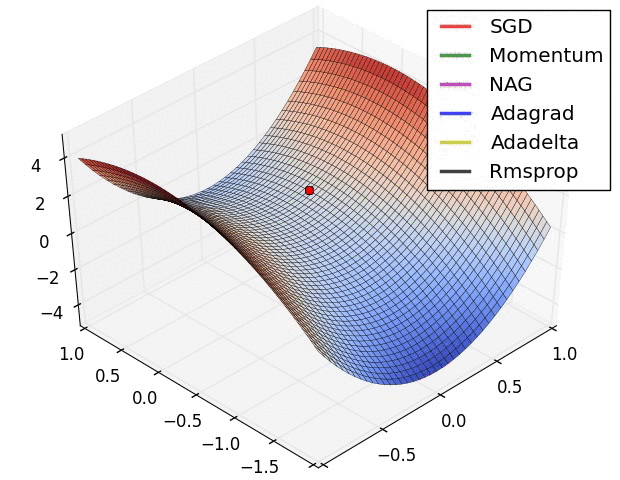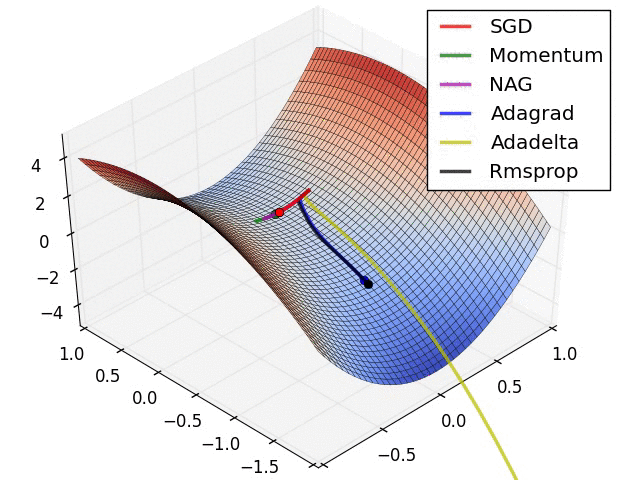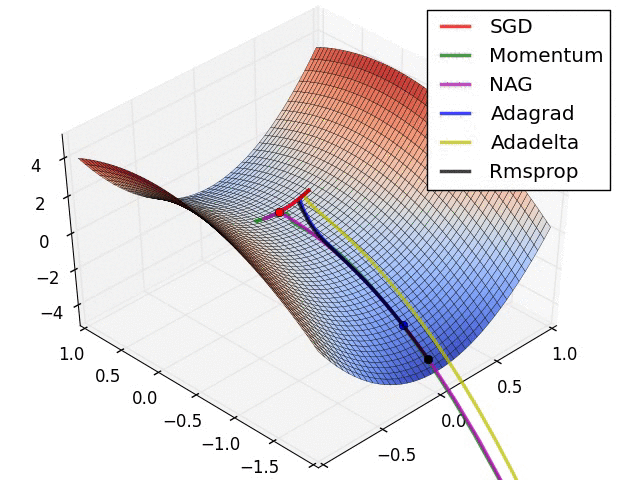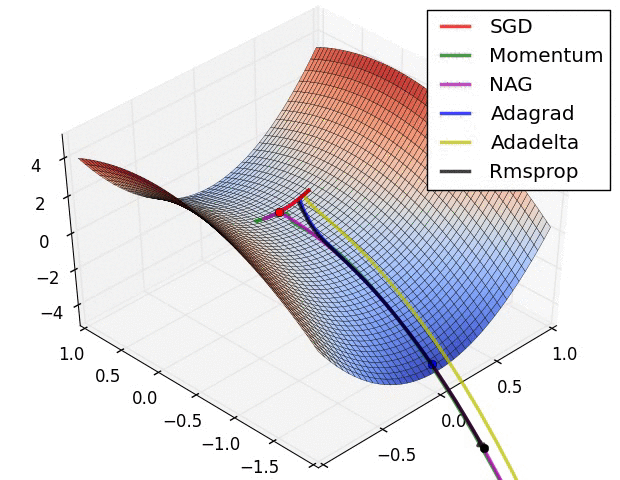
아래 그림은 같은 데이터 , 같은 모델 , 같은 학습률 등 모두 동일한 조건에서 최적화 기법만 다르게 적용했을 때 test 시, 얼마나 잘 예측하고 있는지에 대한 그래프이다.
그래프를 보면 ADAM은 ground-truth와 거의 똑같다.
Momentum같은 경우 거의 잘 예측하긴 했지만, 조금 아쉬운? 모습을 보인다.
SGD 같은 경우 가장 높은 점만 잘 예측하고, 나머지 데이터들에 대해선 거의 맞추지 못하고있다.

이 그래프가 시사하는 바는 무엇일까? 바로 집에 빨리 가고싶다면! 저녁 있는 삶을 원한다면! "ADAM"을 쓰라는 거다.
어떤 최적화 기법을 쓰냐에 따라 성능 혹은 학습 기간이 달라진다.
효율성을 높이기 위해서는 알맞은 최적화 기법을 사용해야된다.
1. Gradient Descent
1) Gradient descent
Day7에서 배웠으니까 간단하게 넘어간다.
1차 미분값을 이용해 함수의 local minimum을 찾아가는 방법을 애기한다.

x라는 점에서의 cost함수의 미분계수값을 통해 x를 업데이트해가며 cost함수가 최소일 때를 찾는 기법이다.
Train Data를 전부 다 쓰기 때문에 Batch Gradient descent라고도 한다.
모든 데이터를 다 쓰기 때문에 학습이 오래걸리고 local minimum을 보장하기 때문에 잘 쓰지 않는다.
2) Stochastic Gradient Descent (SGD)
BGD와 전체적인 방법은 비슷하나, 랜덤으로 하나의 데이터(single sample)에 대해서 경사를 업데이트한다.
BGD와는 다르게 웬만하면 global minimum을 보장한다. 그 이유는 Day7에 써있음. 비교했을 때, 속도가 더 빠르긴 하지만 다른 기법들과 비교했을 땐 느린 편이고, 학습이 불안정하다.
3) Mini batch Gradient Descent (MGD)
전체 데이터를 mini-batch의 크기만큼 나눈 후, mini-batch에 대해서 경사를 업데이트한다.
위의 기법들보다는 MGD가 더 성능이 좋다고 한다. 하지만 batch size를 잘 정해야한다.
On Large-batch Training for Deep Learning: Generalization Gap and Sharp Minima, 2017 논문에 의하면
"large batch methods tend to converge to sharp minimizers of the training and testing functions.
In contrast, small-batch methods consistently converge to flat minimizers..." 라고 써있다.
영어를 보니 살짝 현기증이 오는데 결론은 small mini-batch가 좋다 이거다.

flat한 곳에서 수렴한다면 training과 test 차이가 날 때, 극솟값의 차이가 얼마나지 않지만 , sharp minimum에서는 굉장히 큰 차이가 나게 된다.
그래서 결론은 mini-batch의 사이즈는 작아야 좋다는 건데 보통 2의 지수승으로 설정을 한다.

예시 ) 총 데이터가 100개일 때,
100개에 대해 경사를 업데이트 -> BGD
1개에 대해 경사를 업데이트 -> SGD
10 (mini-batch size)개에 대해 경사를 업데이트 -> MGD
기초적은 Gradient descent말고 다른 방법들을 살펴보자.
2. Momentum
쉽게 말하면 , "관성"으로 이전에서 학습하던 방향을 일부 수용해 경사를 업데이트하는 방식이다.
이전에 움직이던 방향을 어느정도 고려해 이번에 움직일 방향을 결정하겠다는 뜻이다.

학습하던 방향을 알기 위해서는 이전 경사들의 방향에 대해 알아야한다.
경사를 업데이트할 때, 현재 데이터에 대한 gradient값 대신 gradient값+ $\beta$ *이전 값들의 합을 빼줘 경사를 업데이트해준다.
(음,,머리로는 알겠는데 말로 설명하려니 너무 어렵다,,,)
이때 $\beta$가 momentum으로 하이퍼파라미터로 우리가 원하는 값을 지정해주면 되는데 0.9가 국룰인 거 같다.
블로그 에서 참 멋지게 설명해주고 있는데, 이전 경사들을 고려해주기때문에 속력이 아닌 속도가 된다고 한다.
이런 점 덕분에 local minimum이나 saddle point(안장점)을 탈출할 수 있다고 한다.
(saddle point 미분기하 공부할 때 마지막으로 본 친구인데 오랜만,,,)

하지만 이동을 멈춰야하는 지점에 도달해도 momentum에 의해 그 점을 지나칠 수 있다는 문제가 있다.
이러한 문제점을 해결하기 위해 NAG가 제시되었다.
3. Nesterov Accelerated Gradient (공부가 좀 더 필요)

momentum은 현재 데이터에서의 gradient값($\beta$$a_{t}$)에 이전 방향($g_{t}$)을 더해 경사를 업데이트했다.
Nesterov Accelerated Gradient에서는 momentum만큼 경사가 업데이트가 되었다고 가정한 후 gradient를 계산하고 이것과 momentum을 합해 진짜로 경사를 업데이트한다.
이런 방식은 현재의 가속도를 어느정도 고려해 속도를 설정한다고 생각할 수 있다.

이 전 시리즈는 모든 파라미터에 대해 learning rate가 동일하다. 학습률을 파라미터마다 다르게 해주면 어떨까?하는 생각에서 Ada 시리즈가 등장하게 된다.
4. Adagrad
Adagrad는 많이 업데이트 된 파라미터는 learning rate를 작게, 많이 업데이트 되지 않았던 파라미터들은 learning rate를 크게 설정한다. 이 업데이트 됐다는 뜻은 optimum의 근처에 있을 확률이 높다는 뜻이므로 learning rate를 낮추어 아주 조금씩 세밀하게 봐주는 것이다.

\begin{align}g_{ij}^{(t)} = g_{ij}^{(t-1)} + \left( \frac{\partial L}{\partial w_{ij}^{(t)}} \right)^2\end{align}
경사제곱의 합($G_{t}$)으로 이 파라미터가 얼마나 많이 업데이트가 되었는지를 표현한다.
특정 파라미터의 $g_{i,j}$ 가 크다면 다른 파라미터들에 비해 많이 업데이트가 되었다는 뜻이다.
$\epsilon $은 혹여나 0으로 나눠주는 상황에 대비해 $10^{-7}$과 같은 아주 작은 값을 더해주는 것이다.
하이퍼파라미터로 주어진 학습률을 $\sqrt{G_{t} + \epsilon}$으로 나눠주어 각 파라미터별로 다른 학습률에 따라 업데이트해준다.
하지만 학습시간이 길어지면 어떻게 될까? $G_{t}$는 누적합이기때문에 시간이 지날수록 점점 커진다.
분모에 위치하기 때문에 G가 점점 커질수록 학습률은 0에 가까워져 업데이트가 이뤄지지않는다.
이런 문제점을 해결하기 위해 Adadelta가 제안된다.
+ adagrad는 학습률을 다른 알고리즘보다는 좀 크게 주어야 한다고 합니당 ~.~
torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)
Exponentially weighted moving average
❗ 이후 설명을 이해하기 위해서는 Exponentially weighted moving average (EWMA)에 대한 개념이 필요하다.
BARO 최승진 교수님한테 설명을 들었을 땐 이해가 잘 안됐는데,,, 다른 분들이 쓰신 글을 보니 이해가 잘 된다.
Exponentially weighted averages (EMA)는 데이터의 이동평균을 구할 때, 오래된 데이터가 미치는 영향을 지수적으로 감쇠하도록 만들어 주는 방법이라고 한다.
쉽게 설명하면 최근에는 높은 가중치를 주면서 오래된 과거에는 낮은 가중치를 주어 모든 데이터를 고려헤주는 거다.\begin{align}v_t = \beta v_{t-1} + (1-\beta)\theta_t\end{align}
앤드류 응 교수님의 강의를 보면
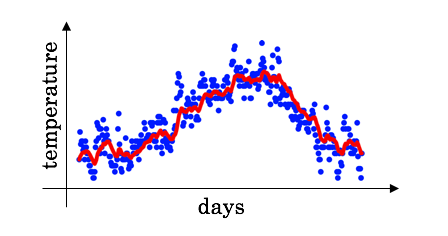
이런 런던 기온의 일별데이터가 있고 이 데이터가 시간의 흐름에 따라 어떻게 변화하는지가 궁금하다.
$\theta$\는 새로 들어온 데이터 이고, v는 현재 경향을 나타내는 값이라고 해보자.
예를 들어 $\theta$\는 2/1의 평균기온 , v는 1/1 ~ 1/31까지의 평균기온의 경향
$\beta$를 만약 0.1이라고 한다면
$v_1 = 0.1 v_0 + 0.9 \theta_1
\\v_2 = 0.1 v_1 + 0.9 \theta_2 = (0.1)^{2}v_0 + 0.1\cdot0.9\theta_1 + 0.9\theta_2
\\ v_3 = 0.1 v_2 + 0.9 \theta_3 = (0.1)^{3}v_0 + (0.1)^{2}\cdot0.9\theta_1 + 0.1\cdot0.9\theta_2 + 0.9\theta_3
\\\vdots
\\ v_n = (0.1)^{n}v_{0} + (0.1)^{n-1}\cdot0.9\theta_{1} + \cdots + 0.9\theta_{n}$
오래된 데이터일수록 $\beta$가 계속 제곱되어 지수적으로 값이 빠르게 감소하는데 이를 "지수적 감쇠"라 부르기 때문에
Exponentiall이라는 이름이 붙은 것 같다.
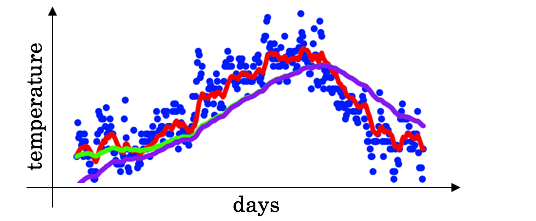
smooth한 그래프가 그려지기 위해서는 $\beta$를 키워줘야하는데 초기구간에는 오차가 존재합니다.
보라색 그래프가 smooth하지만 초기구간을 보면 평균보다 더 낮은 게 보이죠
초기 구간의 bias를 보정하기위해 bias correction이라는 개념이 필요한데 기존 $v_{t}$ 에서 $1- \beta^{t}$를 나눠주면 된다고 합니다.
\begin{align}v(t) := v(t) / (1-\beta^t)\end{align}
5. Adadelta
후 멀고도 멀었습니다... 다시 Adadelta로 돌아오면
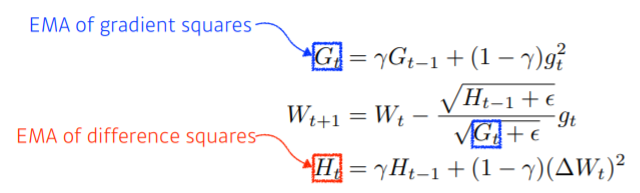
$G_{t}$를 Adagrad와는 다르게 그냥 gradient 제곱의 누적합이 아닌 EMWA 개념을 활용하여 표현해줍니다.
학습률을 곱해줬던 Adagrad와는 다르게 EMWA를 사용한 가중치 변화량의 제곱합의 루트를 씌어 곱해줍니다.
주의할 점은 Adadelta는 학습률이 없습니다! 하지만 torch document에는 있습니다! 띄용;;👀👀 스택오버플로우에 검색해보니 통일성을 위해 넣어놨다고 합니다,,,, lr = 1 로 설정되어있어 모델에 영향을 주지는 않는다고 합니다.
torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)
6. RMSProp
제프리 힌튼 교수님이 논문이 아닌,,,,, 강의 도중 고냥 난 이렇게 하니까 잘되드라? 라고 말씀하셔 사람들이 써봤더니 오 잘되는데? 해서 굳혀진 그런 방법이라고 합니다. 공식을 보면 Adadelta와 Adagrad 딱 그 사이 같습니다,,
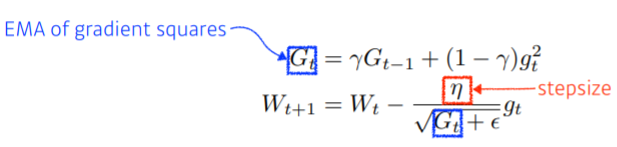
Adagrad의 G를 gradient 제곱의 합을 gradeint 제곱들의 지수 가중 이동 평균으로 표현해주었습니다.
+ 교수님 말에 의하면 $\gamma$= 0.9 , learning_rate = 0.001로 두는 것이 디폴트로 괜찮다고 합니다.
torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
7. Adam
드디어 끝판왕 등장 이제 Adam을 쓸 차례니 저도 집에 갈 수 있을까요???????? 아뇨. 어림도 없습니다.
momentum + adaptive learning rate approch 알고리즘으로 가장 보편적으로 사용됩니다.

❗$m_{t=1}$이 아니고 $m_{t-1}$ 입니다.
momentum의 개념을 이용하지만, $w_{ij}$ 에 대한 momentum인 $m_{ij}$과 learning rate를 조절하는$v_{ij}$는 위와 같이 지수 이동 평균으로 계산됩니다. 좀 특이한 점은 저 $\sqrt{1-\beta}$ 인데 위에서 얘기했던 bias correction을 사용한 것입니다. 위에 t가 붙는 이유는 bias correction 개념을 사용하게 되면 $m_{t} := \frac{ m_{t}}{\sqrt{1-\beta}}$ 로 정의되기 때문에 $\beta$가 결국 t번 곱해지기 때문입니다. 물론 m뿐만이 아니라 v도 동일합니다.
beta1 = 0.9 , beta2 = 0.999 , learning_rate = 1e-3 or 5e-4가 좋다고 합니다. $$
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
Regularization
정규화를 의미하는 Regularization은 overfitting을 피하기 위해 학습을 방해하는 거라고 이해할 수 있다.
딥러닝의 목적은 처음 본 데이터에 대해서도 잘 예측/분류 등을 하는 것이다. 하지만 train 데이터에 너무 적합해져 overfitting 이 일어나게 되면 test 데이터에서는 성능이 안 좋게 나올 수도 있기 때문에 regularization을 사용한다.
1. early stopping

iteration 횟수가 커질수록 training error는 줄어들지만 overfitting이 발생할 수 있다. validation을 적용해 error가 더이상 떨어지지 않는 상태가 유지되다 어느 순간 갑자기 증가하기 전에 학습을 멈추는 것을 early stopping이라고 한다.
말 그대로 더 overfitting이 되기 전에 미리 선수를 쳐서 멈춰버리는거다.
early stopping을 하기 위해서는 별도의 validation set은 필수다
2. parameter norm penalty
weight decay라고도 한다. 이게 함수에 smoothness를 더해준다고 한다.
smooth하게 만들어준다는게 위의 사진을 아래 사진처럼 만들어준다는 뜻 같다.


cost를 단순히 줄이려고만 하면 overfitting이 될 수있다.
그래서 모델의 복잡도를 줄이기(=smooth하게) 위해 , 큰 값을 가지는 파라미터들에게 페널티를 주어 파라미터들이 너무 커지는 것을 방지해준다

패널티 값으로는 주로 L1 regularization 과 L2 regularization을 사용한다.
L1 regularization :
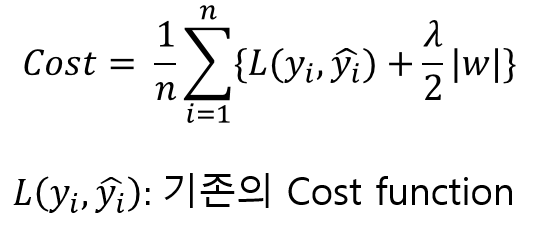
penalty term으로 파라미터 가중치들의 절댓값을 더해줍니다.
L1 loss가 절댓값들의 합이라서 L1 regularization도 절댓값을 더해준 거 같습니다
보너스로 L1 regularization 을 사용하는 회귀 모델을 Lasso regression이라고 합니다.
L2 regularization

penalty term으로 파라미터 가중치들의 제곱값을 더해줍니다.
L2 loss가 제곱들의 합이라서 L2 regularization도 제곱값을 더해준 거 같습니다
보너스로 L2 regularization 을 사용하는 회귀 모델을 Ridge regression이라고 합니다.
3. Data Augmentation
: 주어진 한정된 데이터를 늘려주는 작업을 의미합니다.

딥러닝에서 data는 상당히 중요합니다. data가 적을 땐 svm 기법보다 성능이 안좋을 정도로 딥러닝에게 있어서 Data의 양은 정말 중요합니다.

데이터가 한정되어있을 경우 augmentation을 통해 데이터를 늘려주어야합니다.
augmentation의 종류는 엄청나게 많습니다. jittering , scaling , rotate , crop , flip ,hsv 조절 등등,,,
4. Noise Robustness

인풋데이터나 가중치에 랜덤으로 noise를 섞어준다.
왜 성능이 좋은지는 교수님도 잘,,ㅎㅎ 의문이라고 하신다.
5. Label smoothing

말그대로 label을 좀 풀어준다? 라고 이해하면 된다.
예를 들어 분류문제에서 원핫인코딩을 통해 [0,1,0,0,0] 식으로 나와야 하지만 label smoothing을 통해 [0.5,0.8,0..5,0.5,0.5] 으로 표현해준다. 약간의 noise를 넣어 overfitting을 방지해주는 것이다.
블로그에 의하면 label annotation은 사람이 하기 때문에 실수의 가능성이 있어 ground truth가 100% 정확하지는 않다고 한다. 그래서 label smoothing을 통해 mislabeled data도 잘 학습할 수 있게 해주는 것이라고 한다.

이미지를 섞거나, 이미지의 특정영역을 합쳐서 label smoothing을 한 경우이다. 으,,, 그림 기괴해;
교수님도 이유는 모르겠지만 성능이 아주 좋아 잘 사용하신다고 하셨다.
6. Dropout

dropout_rate를 하이퍼파라미터로 입력받아 그 비율만큼 노드들의 일부를 비활성화시켜준다.
뉴런들이 다 이어져있으면 overfitting의 위험이 있으므로 일부러 연결을 끊어주는 것이다.
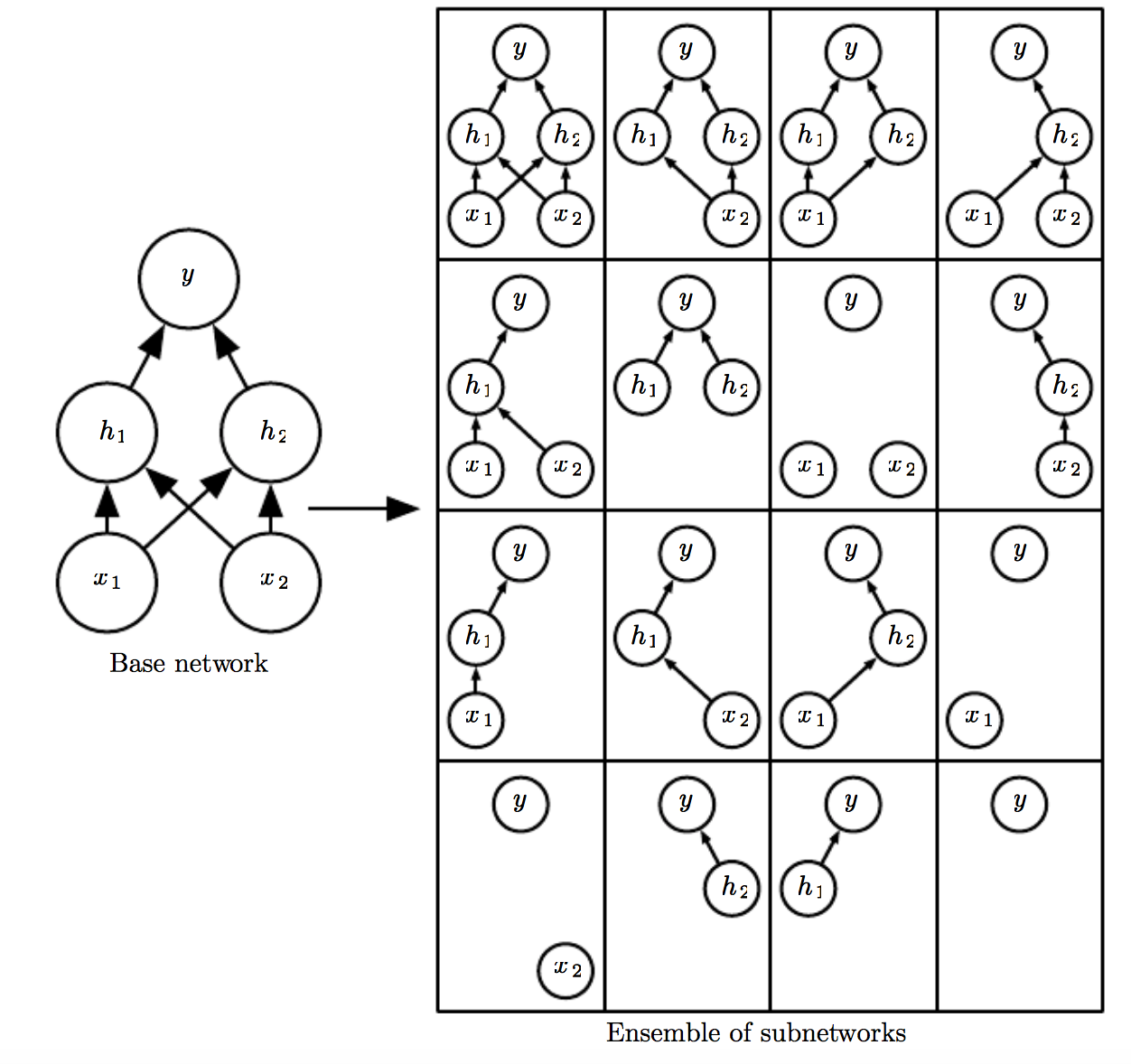
블로그에 의하면 드랍아웃을 통해 여러 모델을 학습시킨 것과 같은 앙상블 효과를 볼 수 있어 overfitting 문제를 해결할 수 있다고 한다.
+ 별 생각 없었는데 드랍아웃이 어떻게 작동하냐는 질문을 듣고 좀 벙쪘다. 그러게?
torch.nn.dropout을 보면 "Each channel will be zeroed out independently on every forward call."라고 써있다.
p의 확률에 따라 랜덤으로 몇 개의 채널의 HW만큼의 픽셀들이 모두 0이 된다.
7. batch normalization
각 미니배치별로 정규화 해주는 기법이다. standardization이라는 표현이 더 맞을 거 같다.
정규화는 평균을 뺀 값을 표준편차로 나눠주면 된다 $\epsilon$은 0을 방지하기 위해 들어간 값이다.
채널과는 독립적으로 배치사이즈 내에서 H,W에 대해서만 계산된다.
데이터 셋 전체를 정규화해주는 것보다는 학습에 사용되는 미니배치별로 정규화 해주는 것이 더 효과가 좋다고 한다.

신경망의 각 layer 마다 활성함수의 출력값을 정규화해주는 작업이다. 일종의 noise를 추가해주는 방법으로 배치마다 정규화를 해주고 또 각 레이어마다 정규화해주기 때문에 초깃값 문제에서 자유로워진다고 한다.

여기서 internal covariate shift를 교수님이 언급해주셨는데, 검색해보니 네트워크의 각 layer마다 인풋데이터의 분산이 달라지는 현상을 얘기한다고 한다. 그래서 이걸 방지하고자 정규화를 했다고하지만 이후 논문들에서는 아님이 밝혀졌다고 한다.
batch normalization은 layer, instance, group 등 친구가 많다,,,

layer Normalization
Batch normalization과 다르게 batch-size에 대해 고민하지 않고 "채널"에 대해 normalizaiton 된다.
batch Normalization같은 경우는 하나의 batch 내에서 인덱스가 같은 channel에 존재하는 weight들끼리 normalization을 한다면, layer Normalization같은 경우는 하나의 데이터에 대해 C개의 채널에 대해서 인덱스가 같은 채널에 존재하는 weight들끼리 normalization을 한다.
Instance Normalization
batch, channel과는 무관하게 하나의 H,W로 이뤄져있는 2차원 weight에 대해서만 normalization을 진행한다.
Group Normalization
하나의 데이터 내에서 총 C개의 채널을 그룹지어 normalization을 진행한다.
2. CNN 맛보기
📌 학습목표
- fully connected layer와 비교해서 CNN(Convolutional Neural Network)의 커널 연산이 가지는 장점과, Convolution 연산이 다양한 차원에서 어떻게 진행되는지를 이해하기
- 커널을 통해 그레디언트가 어떻게 전달이 되는지, 역전파가 어떻게 이루어지는지 이해하기
1. MLP와 Convolution 비교

MLP는 모든 뉴런들이 선형모델과 활성함수로 모두 연결된 fully connected 구조로, 각 픽셀마다 할당된 가중치가 존재한다. 논문을 읽다가 FC layer라고 나오면 MLP를 얘기하는 것이다.
각 성분 $h_{i}$ 에 대응하는 가중치 행 $W_{i}$이 필요하다.
만약 심플하게 x의 사이즈가 1 x N , y의 사이즈가 1 x M 이라면 파라미터의 개수는 N x M개가 필요하다. (bias 무시)

convolution 연산은 MLP와는 다르게 커널이 입력벡터 위에서 움직이며 선형모델과 함성함수로 적용되는 구조다.
행마다 다른 가중치가 곱해지는 MLP와는 다르게 convolution연산에서는 동일한 커널이 위와 같이 움직이며 적용된다. 위와 동일한 x,y에 대해 파라미터의 개수는 x,y사이즈와는 무관하게 커널의 사이즈가 된다.
예를 들어 x = 99 , y = 10일 때, MLP의 경우 파라미터의 개수가 990개가 되지만 conv연산의 경우 커널의 사이즈인 10개가 끝이다... 이렇게 파라미터의 수를 대폭 줄일 수 있다.

MLP에서의 가중치 벡터 W를 input 차원에서 output차원으로의 선형변환으로 볼 수 있다. covolution연산도 마찬가지이다. 마지막에 하는 활성함수를 제외하면 결국 input 차원에서 output 차원으로 바꿔주기때문에 conv 또한 선형변환이다.
2. convolution 연산 이해하기(공부가 더 필요,, 이해가 잘 안간다.)

수학적인 의미는 신호를 커널을 이용해 국소적으로 증폭 또는 감소시켜 정보를 추출 또는 필터링하는 것이다.

커널은 움직이지만 변하지 않는데 이걸 translation invariant라고 한다.
3. 다양한 차원에서의 convolution

데이터의 타입에 따라 사용하는 커널이 달라진다.
예를 들어 음성이나 텍스트 같은 1차원 데이터라면 1D conv를 흑백 사진같은 2차원 데이터라면 2D conv를 컬러 이미지데이터의 경우 3D conv를 이용한다.


3D conv 연산의 경우 커널의 채널 수와 입력의 채널수가 같아야한다.
예를 들어 입력 데이터가 HxWxC = 7x7x3 이라면 size = 3인 커널은 3x3x3이어야한다. 이 경우 output은 5x5x1이 된다.
3x3x3 커널이 10개가 있다면 output은 5x5x10이 된다.
커널의 채널 수는 입력의 채널수와 같아야하고, 커널의 개수는 아웃풋의 채널수와 같다.
4. convolution 연산의 역전파 이해하기

convolution 연산은 커널이 모든 입력데이터에 공통적으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.

conv연산을 할 때 위의 그림에서는 \begin{align}O_{1} = x_{1}w_{1} + x_{2}w_{2} + x_{3}w_{3}
\\O_{2} = x_{2}w_{1} + x_{3}w_{2} + x_{4}w_{3}
\\O_{3} = x_{3}w_{1} + x_{4}w_{2} + x_{5}w_{3}
\end{align} 와 같이 표현된다.
역전파 단게에서 다시 커널을 통해 그레디언트가 전달된다.

위와 같이 입력값에는 해당 커널을 거친 입력값들이 곱해져 전달된다.
각 커널에 들어오는 모든 그레디언트를 더하면 결국 convolution 연산과 같아진다.
\begin{align}\frac{\partial{L}}{\partial{W_{1}}} = \delta_{1}x_{1} +\delta_{2}x_{2} + \delta_{3}x_{3}
\\ \frac{\partial{L}}{\partial{W_{2}}} = \delta_{1}x_{2} +\delta_{2}x_{3} + \delta_{3}x_{4}
\\\frac{\partial{L}}{\partial{W_{3}}} = \delta_{1}x_{3} +\delta_{2}x_{4} + \delta_{3}x_{5}\end{align}

Further study : 시계열의 경우 일반적인 k-fold를 사용해도 될까요?
나의 답은 아니다! 시계열은 sequence한 데이터로 이전 데이터들이 이후 데이터들에 영향을 미치므로 순서가 중요하다.
하지만 k-fold의 경우 k개의 set으로 자른 후 하나의 set은 validation , 나머지set은 train data로 k번 반복한다.
validation set이 시계열에서 앞부분이라면 성능이 좋지 않고, 뒷부분일 때 성능이 좋아질 것이라고 예상된다.
time series가 쓸 수 있는 k-fold가 따로 있다. 바로 Nested cross validation이다.
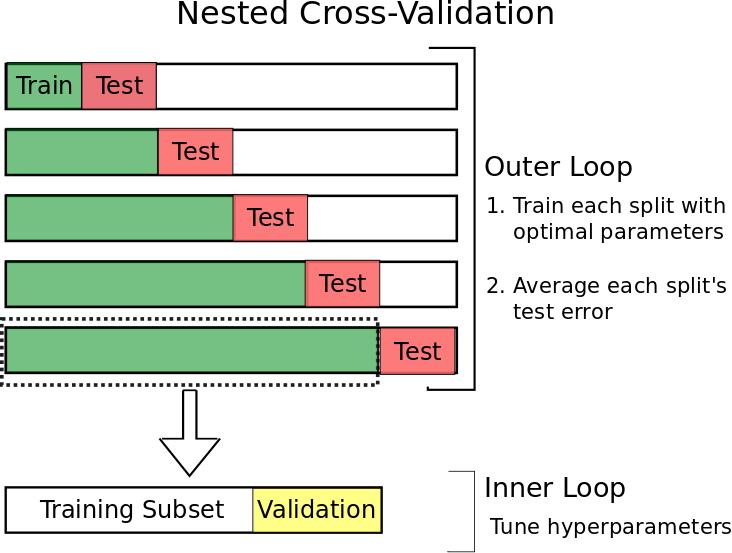
기존의 cross-validation을 중첩한 방식으로 outer loop와 inner loop으로 구성되어있다.
outerloop에는 기존 cross-validation과 같이 validation set 대신 train set과 test set으로 나눠준다.
train set 내에서 inner loop가 작동한다. train set을 다시 train set과 validaion set으로 쪼개고 학습 후 평가하며 파라미터를 튜닝한다. 최종 test error는 각각 fold에 대한 test error의 평균을 사용한다.
validation, test set으로 미래 데이터를 활용하기 때문에 시계열에 적합하다.
피어세션
1. 논문리뷰
보윤님이 발표셨는데 그냥 나한테 도움될 거 같은 내용 받아적었다.
- 모든 흐름은 "어떤 문제를 우리가 어떻게 해결했다. 이게 왜 잘 된다. 그래서 우리 모델이 최고다"
- 첫 장은 논문 제목 + 저자 + 학회가 들어가야된다.
- 목차의 경우 너무 세세하게 쓰면 실수할 수도 있다. 큰 제목만 써도 된다.
- 이전 모델들의 문제점이 해결되었다면 언급해라
- Detail은 이 사람이 얼마나 스마트한가를 보여준다. 사소한 오타 포함
- 설명을 할 거면 끝까지 완벽하게 아니면 간략하게 -> 질문이 나왔을 때 완벽하게 답변하면 된다.
2. 알고리즘 풀이
sen1 = list(input())
sen2 = list(input())
m = len(sen1)
n = len(sen2)
dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
# sen1 단어 하나하나를 sen2와 비교해야 됨 행=sen1 , 열 sen2
for i , word1 in enumerate(sen1) :
for j , word2 in enumerate(sen2):
if word1 == word2 : dp[i+1][j+1] = dp[i][j]+1
else :
dp[i+1][j+1] = max(dp[i][j+1] , dp[i+1][j])
print(dp[m][n]) c , n = map(int,input().split())
arr = []
for _ in range(n): arr.append(list(map(int,input().split())))
#arr[0] = cost , arr[1] = customer
dp = [1000000] * 1101
dp[0] = 0
arr.sort(key = lambda x : x[1])
for i in arr :
cost = i[0]
customer = i[1]
for j in range(1,1101):
if customer <= j : dp[j] = min(dp[j] , dp[j-customer] + cost)
nmin = 1000000
for i in range(c, 1101):
nmin = min(nmin , dp[i])
print(nmin)
3. 선형대수 스터디 : 부분공간의 기저와 차원 - 깃허브에 업로드
오늘 하루 정말 알찼다,,,,,분명 학습정리를 7시부터 시작했는데 벌써 5시다.
교수님께서 언급만 하고 넘어가신 거에 대해 찾아보려했는데 발음이 너무 좋으셔서 잘 못알아들었다;; 이런,,,,
평소에 아무 생각 없이 쓰던 Adam , 그냥 남들이 0.9주던 weight decay 등 아무 생각없이 쓰고 있었던 내가 간과했었던 개념들에 대해 공부했다. 기초를 촥촥촥 다지는 시간이었다.
하지만 코드에 대해 자세히 리뷰를 못해서 아쉽다. 설 연휴에 시간이 나면 코드 리뷰를 해서 다시 재업로드 해야겠다.
피어세션 시간에는 보윤님이 transformer에 대해서 설명해주시고 피드백을 받으셨다.
새삼 보윤님만의 피드백이 아닌 거 같아서 나도 일부 받아적었다. 다음 주 논문 스터디 친구들 만나면 공유해줘야지🥴
velog.io/@minjung-s/Optimization-Algorithm
hyunw.kim/blog/2017/11/01/Optimization.html
light-tree.tistory.com/216 sacko.tistory.com/44
wingnim.tistory.com/92modulabs-biomedical.github.io/Bias_vs_Variance
'Naver Ai Boostcamp' 카테고리의 다른 글
| [DAY 14] Recurrent Neural Networks (0) | 2021.02.05 |
|---|---|
| [DAY 13] Convolutional Neural Networks (0) | 2021.02.04 |
| [DAY 11] 딥러닝 기초 (0) | 2021.02.02 |
| [DAY 10] 시각화 / 통계학 (0) | 2021.01.30 |
| [DAY 9] Pandas II / 확률론 (0) | 2021.01.29 |