경사하강법 (순한 맛)
📌 미분
- 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
- 최적화에서 많이 사용하는 기법이다.
- 도함수 = 접선 -> x에서의 접선의 기울기 = 점 x에서의 미분 값
- 함숫값을 증가시키고싶다면 ? x ≔ x + f'(x)
함숫값을 감소시키고싶다면 ? x ≔ x - f'(x)

- x ≔ x + f'(x) : 미분값을 더하는 경사상승법 , 극댓값의 위치를 구할 때 사용
- x ≔ x - f'(x) : 미분값을 빼면 경사하강법 , 극솟값의 위치를 구할 때 사용
- 우리의 목적은 "cost함수의 최소화" 그러므로 cost함수의 최솟값을 구하기 위해 경사하강법을 사용
- 극솟값을 어떻게 찾을까? (단편적인 2차원 cost함수라고 가정)
1. 우선 한 점 X를 찍는다. (initialize)
2. X에서의 미분값을 구한다.
3. 0이 아니라면 X ≔ X - 미분값 을 찍는다.
4. 미분값이 0이 될 때까지 2~3번 과정을 반복한다
위 과정을 코드로 짜면 아래와 같다.
컴퓨터로 계산할 때는 정확하게 0이 되기 어렵기때문에 0에 근사한 eps 값을 준다. 일종의 threshold
var = init # 초기값 x
grad = gradient(var) # x에서의 미분 값
while(abs(grad) > eps):
var = var - lr*grad
grad = gradient(var)✨👀 lr : 학습률로 미분을 통해 새로운 x를 찍는 즉 업데이트 해주는 속도를 조절한다.
📌다변수 함수의 미분
- 다변수 함수라면 각 변수마다의 편미분을 이용한다.
- 각 변수별로 편미분을 계산한 그래디언트 벡터를 이용 -> 동시에 업데이트 가능

📌 그레디언트 벡터
- $\nabla$는 가장 빨리 증가하는 방향

- -$\nabla$ : 가장 빨리 감소하는 방향 (우리가 알아야하는 것)

$\nabla$ 와 -$\nabla$ 의 차이가 궁금했는데 명확하게 이해됐다.
- 극솟값을 찾는 방법은 일변량 함수일 때와 동일하다.
하지만 벡터일 때는 절댓값대신 norm을 사용해 계산한다.
var = init # 초기값 x
grad = gradient(var) # x에서의 미분 값
while(norm(grad) > eps):
var = var - lr*grad
grad = gradient(var)
📌선형회귀분석 복습
- 유사역행렬을 이용해도 되지만 , ML에서의 비선형도 고려해 일반화된 최적화 기법으로 경사하강법 사용
- 목적 : COST 함수의 최소화 = $|y-x\beta|$를 최소화시켜주는 $\beta$ 찾기

증명 ]

- 일변수함수일때와 마찬가지로 학습률 * 미분값으로 $\beta$를 업데이트해가면된다.
하지만 n차원에서는 극값이 0이 되는 곳을 찾기가 어렵기 때문에 종료시점을 정해준 후 , 반복한다.
for t in range(T):
error = y - X @beta
grad = - X.T @ error
beta = beta - lr*grad
- 업데이트 속도를 조절해주는 학습률은 학습에 큰 영향을 미친다.
학습률이 너무 작으면 수렴하는데까지 시간이 너무 오래걸리고
학습률이 너무 크면 학습이 불안정해 수렴하지 못한다.
뭐든 "적당"한 게 중요하다.ㅎㅎ
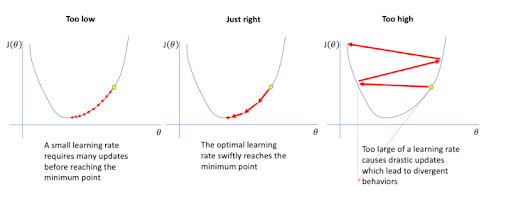
- 함수가 convex할 때는 최솟값 = 극솟값이므로 적절한 학습률 & 학습횟수만 있다면 무조건 수렴한다.
선형회귀의 경우 convex 하므로 경사하강만으로도 수렴가능!
하지만 ML에서는 비선형회귀 (non-linear) 의 경우가 훨씬 많다.

극솟값을 보장할 뿐, 최솟값을 보장할 수 없다. 그렇기에 inital을 어떻게 잡느냐에 따라 수렴값이 달라진다.


📌 확률적 경사 하강법 (stochastic gradient descent)
- 경사하강법과 달리 모든 데이터를 다 사용하지 않고 , 데이터 한 개 또는 일부를 활용하여 업데이트하는 경사하강법을 얘기한다.
- 보통 batch_size = 1 일 때, 확률적 경사하강법(SGD)라고 한다.
전체 데이터 중 랜덤으로 하나의 데이터로 학습 후 업데이트한다. - 일부 데이터 값을 이용하여 만든 목적식은 모든 데이터를 이용하여 만든 목적식과는 다르다.
임시 목적식 , 진짜 목적식 이라고 하겠다.
하지만 일부 데이터 값을 이용한 임시 목적식의 기댓값은 진짜 목적식에 근사한다는 보장이 있다.
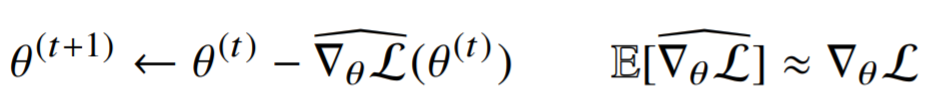
- 업데이트를 할 때마다 , 데이터가 달라지므로 목적식이 계속 조금씩 달라진다.

📌 SGD가 최솟값을 보장할 수 있는 이유

확률적으로 데이터를 선택하고 , 그 데이터에 맞추어 목적식을 만들게 되므로 매번 목적식이 바뀌게 된다.
예를 들어 , t step 시 , $\theta$에서의 목적값이 0이었다고 해보자. 물론 이때는 극소였겠지만
t+1 step시 , 목적함수가 또 변하므로 이때는 $\theta$에서 목적값이 0이 아닐 것이다. (물론 같을 수도 있겠지!)
이런식으로 local minumum에 빠지지 않고 최솟값을 찾아갈수 있다.
- 하지만 랜덤하게 데이터를 선택하기 때문에 , 학습과정에서 진폭이 크고 불안정하고 오차가 크고 gpu의 성능을 십분 활용하지 못한다고 한다. -> 이를 보완하기 위해 미니배치경사하강법도 사용됨.

피어세션
오늘도 백준에서 알고리즘 문제 풀이를 진행했다.
각자 코드를 리뷰하고, 시간을 재고 문제를 풀었다.
bfs & dfs 같은 경우 풀이법이 거기서 거기라 그런지 거의 다 비슷했던 듯 하다.
백준 2606 바이러스
from collections import deque
computers = int(input())
network = int(input())
graph = [[]for _ in range(computers+1)]
visited = [False for _ in range(computers+1)]
for _ in range(network):
a, b = map(int,input().split())
graph[a].append(b)
graph[b].append(a)
cnt = 0
q = deque([1])
visited[1] = True
while q :
cur = q.popleft()
cnt += 1
for node in graph[cur]:
if not visited[node]:
q.append(node)
visited[node] = True
print(cnt-1)백준 2644 촌수계산
from collections import deque
v = int(input())
start, end = map(int, input().split())
e = int(input())
graph = [[]for _ in range(v+1)]
visited = [0 for _ in range(v+1)]
for _ in range(e):
a, b = map(int,input().split())
graph[a].append(b)
graph[b].append(a)
q = deque([start])
visited[start] = 1
answer = 0
while q :
cur = q.popleft()
if cur == end :
answer = visited[end]
break
for node in graph[cur]:
if not visited[node]:
q.append(node)
visited[node] = visited[cur] + 1
print(answer - 1)
오늘의 소감
피곤하다.
오늘 논문 스터디에서 yolo 발표하는 날인데 준비한다고 이틀 내내 많이 못잤더니 너무 피곤하다.
근데 또 역설적이게 피곤하니까 좀 사람 사는 거 같다. ㅎㅎ
오늘도 수학이라서 편한 마음으로 들으려다가 공식증명에서 꽤 애먹었다.
하지만 저번주에 미리 예습해놨어서 경사하강법이 매운 맛은 아니었다. 그냥 뭐 팔도비빔면 수준 ^^
평소 논문을 읽을 때도 SVD,,,? 흠,, 선대 공부해야되는데,,, 하다가 오늘 공식 증명을 하면서 공부를 할 필요를 느꼈다.
그래서 "선형대수학 스터디"를 개설했다. 내가 스터디 슬랙 퍼블땀ㅋㅎ 뿌듯행
'Naver Ai Boostcamp' 카테고리의 다른 글
| [DAY 9] Pandas II / 확률론 (0) | 2021.01.29 |
|---|---|
| [DAY 8] Pandas I / 딥러닝 학습방법 이해하기 (0) | 2021.01.27 |
| [DAY 6] Numpy / 벡터 / 행렬 (0) | 2021.01.26 |
| [DAY 5] 파이썬으로 데이터 다루기 (0) | 2021.01.23 |
| [DAY 4] 파이썬 기초 문법 III (1) | 2021.01.21 |