요새 넘나 소홀했던 거 ㅇㅈ
그래서 반성하는 마음으로 알고리즘 스터디 한 당일 날 배운 알고리즘을 정리한당,,,흑,,,
앗 스터디장님이 새로 바뀌셨다. 기존 상규님이 갓카오에 합격하는 바람에 녹형님이 새로운 스터디장이 되셨다.
상규님이 하시는 모든 일 다 잘됐으면 좋겠다 ㅎㅣㅎ
'
배낭 알고리즘은 다이나믹프로그래밍 dp 유형 중 하나다.
도둑이 보석가게에 배낭을 메고 침입했다.
배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 찢어질 것이다.
각 보석들의 무게와 가격은 알고 있다.
배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?

가방의 최대 용량은 10kg 이고 현재 보석은 이렇게 6개가 있다고하자.
그러면 6개 중 10kg를 넘지 않게 잘 골라서 가장 비싼 것들을 골라야한다.
그래서 요런 dp 2차원 배열을 이용해서 해결하려고 한다.
i 번째 보석에 대해서 최대 무게인 10kg가 되기전까지의 최대 값어치를 저장한다.
즉, dp[i][j] : jkg에 담을 수 있는 보석들의 무게인데 , 1 ~ i번째 보석만을 이용해야한다.
예를 들어 dp[3][7] 이면 1~3번 보석을 이용해서 만들 수 있는 7kg 조합 중 가장 비싼 조합 을 저장하는거다.
그럼 how? 그걸 어떻게 할 거냐가 문제다.
1) 우선 1번째 보석이 4kg 짜리 6 달러라고 하자.
그럼 새로 들어온 보석의 무게인 4보다 작은 j들에 대해서는 아무것도 할 수 없다.
즉, 새로운 보석의 무게보다 작은 j 들에 대해서는 보석이 새로 들어오기 전의 최댓값과 보석이 새로 들어온 후 의 최댓값이 같다는 얘기다.
그럼 1번째 보석에 대해서 0~3kg (dp[1][0] ~dp[1][3])는 보석이 하나도 들어오지 않은 (dp[0][0] ~dp[0][3]) 와 같다.
j =4 부터는 새로운 보석 6을 더한 게 0보다 크니깐 6으로 업그레이드가 된다.
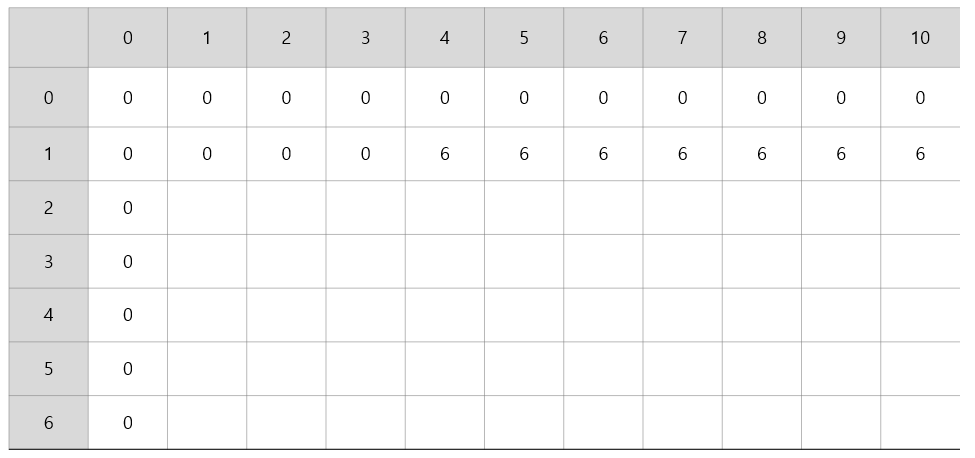
2) 2번째 보석이 4kg 짜리 7달러라고 하자.
똑같이 4kg 이하에 대해서는 0이다.
dp[2][4] 를 생각해보면
4kg 기준 , 1번째 보석을 가지고 만들 수 있는 최댓값은 6 이었다.
하지만 1번째 보석을 쓰지 않고 , 2번째 보석을 사용하면 7이므로 더 크다.
그래서 최댓값은 7이어야된다.
즉, 2번째 보석을 쓰지 않으려면 무게가 0kg이어야된다.
1번째 보석을 쓰면서 0kg 일 떄의 최댓값은 0이다. 거기다 2번째 보석을 더해주면 값어치는 7로 더 커진다.

3) 3번째 보석이 2kg 짜리 4달러라고 하자.

4달러 2kg 짜리인 3번째 보석을 사용해서 총 4kg를 채워야한다고 생각해보자~
그럼 (1,2번째 보석을 이용해서 만들 수 있는 2kg 중 최댓값) + 3번째 보석 2kg 이다.
이걸 dp로 표현해보자면 dp[3][4] = dp[2][2] + 2
핵심은 뭐냐면 값어치 v ,무게 w를 가지는 새로운 i번째 보석이 왔을 때 ,
i번째 보석을 사용하지 않고 최대값을 유지하는 방법 : dp[i-1][j]
i번째 보석을 사용하고 최댓값을 유지하는 방법 : dp[i-1][j-w] + v
둘 중 뭐가 최대인지 골라야한다는 얘기이다.
난 이렇게 이해해버려따. 그리고! 백준 12865번을 푸러따 (www.acmicpc.net/problem/12865)
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<pair<int, int>> bag;
vector<vector<int>> dp;
int main() {
int n, k;
cin >> n >> k;
bag.resize(n + 1);
for (int i = 1; i <= n; i++) {
int w, v;
cin >> w >> v;
bag[i] ={ w,v };
}
dp.resize(n + 1, vector<int>(k + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= k; j++) {
if (j < bag[i].first) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - bag[i].first] + bag[i].second);
}
}
cout << dp[n][k];
}엄청 어려워보였던 문제가 이렇게 30줄 가량으로 풀려버리는게 넘모 신기해,,,
'알고리즘 > 자료구조 & 알고리즘 개념정리' 카테고리의 다른 글
| 2주차 자료구조 - 이진트리 삽입,탐색,삭제,순회 (0) | 2020.12.12 |
|---|---|
| 1주차 자료구조 스터디 - 스택과 큐 (0) | 2020.12.05 |
| c++ 알고리즘 스터디 2주차 - 크루스칼 알고리즘 (0) | 2020.11.26 |
| c++ 알고리즘 스터디 2주차 - 유니온파인드 (0) | 2020.11.26 |
| 알고리즘 스터디 1주차 - 투 포인터 (two pointer) (0) | 2020.11.15 |